题目内容
(2012•道里区一模)在△ABC中,∠ACB=90°,点P和点D分别在边AB和边AC上,且PC=PD.
(1)如图1,当tanB=1时,请写出线段CD与线段PB数量关系:
(2)如图2,当tanB=2时,求证:2BC=AD+
PB.
(3)如图3,在(2)的条件下,若点B关于直线CP对称点E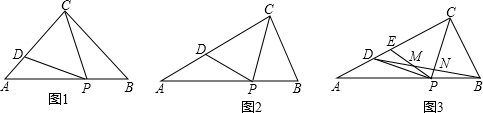 恰好落在边AC上,连接PE、BD,BD分别交PE、CP于M、N两点,且AD=2.求线段MN的长.
恰好落在边AC上,连接PE、BD,BD分别交PE、CP于M、N两点,且AD=2.求线段MN的长.
(1)如图1,当tanB=1时,请写出线段CD与线段PB数量关系:
(2)如图2,当tanB=2时,求证:2BC=AD+
4
| ||
| 5 |
(3)如图3,在(2)的条件下,若点B关于直线CP对称点E
 恰好落在边AC上,连接PE、BD,BD分别交PE、CP于M、N两点,且AD=2.求线段MN的长.
恰好落在边AC上,连接PE、BD,BD分别交PE、CP于M、N两点,且AD=2.求线段MN的长.分析:(1)首先过点P分别作PH⊥AC于点H,PF⊥BC于点F,又由在△ABC中,∠ACB=90°,易得四边形PFCE是矩形,即可得CH=PF,又由tanB=1,可得∠B=45°,PF=BF,由三角函数可求得PF═
PB,由PC=PD,根据三线合一的性质,可得CD=2CH=2PF,即可求得答案;
(2)证明方法同(1),首先可得四边形PFCE是矩形,CH=PF=
CD,然后由勾股定理得:BP=
BF,PF=
BP,即可求得答案;
(3)据题意可得CP是线段BE的垂直平分线,即可得CE=CB,PE=PB,则可求得∠BCP=∠ECP=
∠ACB=45°,然后利用勾股定理,借助于方程求解即可BC=3,AC=2BC=6,AB=3
,AP=2
,CD=4,DE=1,EA=3,然后过点D作AB的平行线分别交EP于点Q,交CP于点R,利用相似三角形的对应边成比例,即可求得答案.
| ||
| 2 |
(2)证明方法同(1),首先可得四边形PFCE是矩形,CH=PF=
| 1 |
| 2 |
| 5 |
2
| ||
| 5 |
(3)据题意可得CP是线段BE的垂直平分线,即可得CE=CB,PE=PB,则可求得∠BCP=∠ECP=
| 1 |
| 2 |
| 5 |
| 5 |
解答:解:(1)CD=
PB.
理由:过点P分别作PH⊥AC于点H,PF⊥BC于点F,
∴∠PHC=∠PFC=90°,
∵∠BCA=90°,
∴四边形PFCE是矩形,
∴CH=PF,
∵PD=PC,
∴CH=
CD,
在Rt△PBF中,tanB=1,
∴PF=BF,
∴PF=PB•sin45°=
PB,
∴CD=2CH=2PF=2×
PB=
PB;

(2)证明:过点P分别作PH⊥AC于点H,PF⊥BC于点F,
∴∠PHC=∠PFC=90°,
∵∠BCA=90°,
∴四边形PFCE是矩形,
∴CH=PF,
∵PD=PC,
∴CH=
CD,
在Rt△PBF中,tanB=2,
即
=2,
∴PF=2BF,
由勾股定理得:BP=
BF,PF=
BP,
∴CH=
BP,CD=
BP,
在Rt△ABC中,tanB=2,
同理可得:AC=2BC,
∵AC=AD+CD,
∴2BC=AD+
BP;
(3)连接BE,
∵点B关于直线CP的对称点为E,
∴CP是线段BE的垂直平分线,
∴CE=CB,PE=PB,
∴∠BCP=∠ECP=
∠ACB=45°,
过点P作PF⊥BC于点F,
设PB=a,
由(2)得:2BC=AD+
BP,
则BC=1+
a,
在Rt△CPF中,∠FCP=45°,PF=CF=
a,
而BF=
BP=
a,
由CF+BF=BC得,
a+
a=1+
a,
解得:a=
,
即BP=
,
∴BC=3,AC=2BC=6,AB=3
,AP=2
,CD=4,DE=1,EA=3,
∴BD=
=5,
过点D作AB的平行线分别交EP于点Q,交CP于点R,
由△EDQ∽△EAP,得ED:EA=DQ:AP=1:3,得DQ=
,
由△QDM∽△PBM,得DM:BM=QD:PB=2:3,得DM=
BD=2,
由△CDR∽△CAP,得DR:AP=CD:CA=4:6,得DR=
,
由△NDR∽△NBP,得DN:BN=DR:PB=
:
=
,得DN=
BD=
,
∴NM=DN-DM=
-2=
.
| 2 |
理由:过点P分别作PH⊥AC于点H,PF⊥BC于点F,
∴∠PHC=∠PFC=90°,
∵∠BCA=90°,
∴四边形PFCE是矩形,
∴CH=PF,
∵PD=PC,
∴CH=
| 1 |
| 2 |
在Rt△PBF中,tanB=1,
∴PF=BF,
∴PF=PB•sin45°=
| ||
| 2 |
∴CD=2CH=2PF=2×
| ||
| 2 |
| 2 |

(2)证明:过点P分别作PH⊥AC于点H,PF⊥BC于点F,
∴∠PHC=∠PFC=90°,
∵∠BCA=90°,
∴四边形PFCE是矩形,
∴CH=PF,
∵PD=PC,
∴CH=
| 1 |
| 2 |
在Rt△PBF中,tanB=2,
即
| PF |
| BF |
∴PF=2BF,
由勾股定理得:BP=
| 5 |
2
| ||
| 5 |
∴CH=
2
| ||
| 5 |
4
| ||
| 5 |
在Rt△ABC中,tanB=2,
同理可得:AC=2BC,
∵AC=AD+CD,
∴2BC=AD+
4
| ||
| 5 |
(3)连接BE,
∵点B关于直线CP的对称点为E,
∴CP是线段BE的垂直平分线,
∴CE=CB,PE=PB,
∴∠BCP=∠ECP=
| 1 |
| 2 |
过点P作PF⊥BC于点F,
设PB=a,
由(2)得:2BC=AD+
4
| ||
| 5 |
则BC=1+
2
| ||
| 5 |
在Rt△CPF中,∠FCP=45°,PF=CF=
2
| ||
| 5 |
而BF=
| ||
| 5 |
| ||
| 5 |
由CF+BF=BC得,
2
| ||
| 5 |
| ||
| 5 |
2
| ||
| 5 |
解得:a=
| 5 |
即BP=
| 5 |
∴BC=3,AC=2BC=6,AB=3
| 5 |
| 5 |
∴BD=
| CB2+CD2 |
过点D作AB的平行线分别交EP于点Q,交CP于点R,
由△EDQ∽△EAP,得ED:EA=DQ:AP=1:3,得DQ=
2
| ||
| 3 |
由△QDM∽△PBM,得DM:BM=QD:PB=2:3,得DM=
| 2 |
| 5 |
由△CDR∽△CAP,得DR:AP=CD:CA=4:6,得DR=
4
| ||
| 3 |
由△NDR∽△NBP,得DN:BN=DR:PB=
4
| ||
| 3 |
| 5 |
| 4 |
| 3 |
| 4 |
| 7 |
| 20 |
| 7 |
∴NM=DN-DM=
| 20 |
| 7 |
| 6 |
| 7 |
点评:此题考查了相似三角形的判定与性质、矩形的判定与性质、勾股定理、等腰三角形的性质、直角三角形的性质以及三角函数等知识.此题综合性很强,难度很大,注意辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
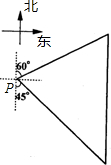 (2012•道里区一模)如图,一艘渔船位于海洋观测站P的北偏东60°方向,渔船在A处与海洋观测站P的距离为80 海里,它沿正南方向航行一段时间后,到达位于海洋观测站P的南偏东45°方向上的B处.则此时渔船所在的B处与海洋观测站P的距离为
(2012•道里区一模)如图,一艘渔船位于海洋观测站P的北偏东60°方向,渔船在A处与海洋观测站P的距离为80 海里,它沿正南方向航行一段时间后,到达位于海洋观测站P的南偏东45°方向上的B处.则此时渔船所在的B处与海洋观测站P的距离为 (2012•道里区一模)如图,新城小区计划用铁栅栏围建一个矩形的车棚ABCD,为了方便存车,在CD边上开了一个lm宽的门,在BC边上开了一个2m宽的门(门不是用铁栅栏做成的).设AB边长为x(m),AD边长为y(m),且AB<AD.
(2012•道里区一模)如图,新城小区计划用铁栅栏围建一个矩形的车棚ABCD,为了方便存车,在CD边上开了一个lm宽的门,在BC边上开了一个2m宽的门(门不是用铁栅栏做成的).设AB边长为x(m),AD边长为y(m),且AB<AD.