��Ŀ����
��2012•������һģ����ͼ����ABC��A��
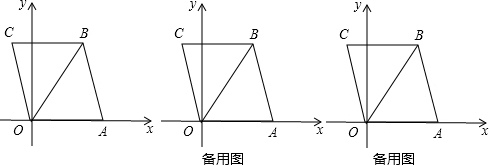
��0����B��3��4��������ABO����ֱ��OB���ۣ���A���ڵڶ������ڵĵ�C��
��1�����C�����ꣻ
��2������P�ӵ�0������5����λ������ٶ���OB���յ�B�˶�������AP��������AP���ŵ�A��ʱ����ת��y�ύ��һ��Q������ת�Ǧ�=
��OAB�����߶�0Q�ij�Ϊd����P�˶���ʱ��Ϊt�룬��d��t�ĺ�����ϵʽ��ֱ��д��ʱ��t��ȡֵ��Χ����
��3���ڣ�2���������£�����CP����P���˶��Ĺ����У��Ƿ����CP��AQ�������ڣ����ʱt��ֵ�����жϵ�B���Ե�PΪԲ�ģ�0Q��Ϊ�뾶�ġ�P��λ�ù�ϵ���������ڣ���˵�����ɣ�
| 25 |
| 6 |
��1�����C�����ꣻ
��2������P�ӵ�0������5����λ������ٶ���OB���յ�B�˶�������AP��������AP���ŵ�A��ʱ����ת��y�ύ��һ��Q������ת�Ǧ�=
| 1 |
| 2 |
��3���ڣ�2���������£�����CP����P���˶��Ĺ����У��Ƿ����CP��AQ�������ڣ����ʱt��ֵ�����жϵ�B���Ե�PΪԲ�ģ�0Q��Ϊ�뾶�ġ�P��λ�ù�ϵ���������ڣ���˵�����ɣ�

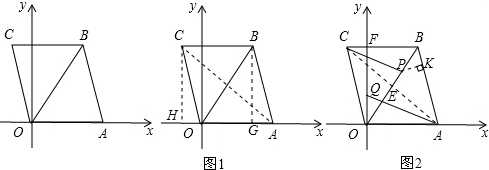
��������1����C��x��y�������������ľ��빫ʽ������õ�C�����ꣻ
��2����ͼ1������AC������B��BG��x���ڵ�G������C��CH��x���ڵ�H����Ҫ�������ۣ���0��t��
��
��t��1ʱ����������µ�d��t�ĺ�����ϵʽ��ֱ��д��ʱ��t��ȡֵ��Χ����
��3����ͼ2������P��PK��AB�ڵ�K���������CP��AQ������ƽ���ߵ����ʡ���ת��������֪PE=PK��Ȼ������߶μ��������ϵ������ô�ʱ��t��ֵ��
���жϵ�B���Ե�PΪԲ�ģ�0Q��Ϊ�뾶�ġ�P��λ�ù�ϵ��ֻ��֤����B��Բ��P�ľ����Ƿ���ڡ�P�İ뾶���ɣ�
��2����ͼ1������AC������B��BG��x���ڵ�G������C��CH��x���ڵ�H����Ҫ�������ۣ���0��t��
| 1 |
| 2 |
| 1 |
| 2 |
��3����ͼ2������P��PK��AB�ڵ�K���������CP��AQ������ƽ���ߵ����ʡ���ת��������֪PE=PK��Ȼ������߶μ��������ϵ������ô�ʱ��t��ֵ��
���жϵ�B���Ե�PΪԲ�ģ�0Q��Ϊ�뾶�ġ�P��λ�ù�ϵ��ֻ��֤����B��Բ��P�ľ����Ƿ���ڡ�P�İ뾶���ɣ�
��� �⣺��1����C��x��y����x��0��y��0����
�⣺��1����C��x��y����x��0��y��0����
��A��
��0����B��3��4����
��OA=
��AB=
=
��
�߽֡���ABO����ֱ��OB���ۣ���A���ڵڶ������ڵĵ�C����
��OA=OC��AB=CB��
��
��
���
��
���C�������ǣ�-
��4����
��2����ͼ1������AC������B��BG��x���ڵ�G������C��CH��x���ڵ�H��
��A��
��0����B��3��4����
��OA=
��OG=3��BG=4��
��AG=
��
��AC=
�����ɶ�������
��AE=
��
ͬ����OE=
��
�ٵ�0��t��
ʱ��
��OP=5t��
��PE=
-5t��
��
=
��
��d=-
t+
��
�ڵ�
��t��1ʱ��ͬ����d=
t-
��
��3����ͼ2������P��PK��AB�ڵ�K��
��CP��AQ��
���PCE=��QAE��
��AE=CE��AC��BO��
��PC=PA��
���PAE=��PCE=
��QAE=��PAQ��
���PAB=��QAE��
���PAE=��PAB��
��PE=PK��
��������ABCO����PBK=��OBF��
��sin��PBK=sin��OBF=
=
=
��
��OP=5t��OB=5��
��PE=
-5t��PB=5-5t��
��
=
��
��ã�t=
��
�����CP��AQ����ʱt=
��
��
��
��1��
��t=
ʱ��OQ=d=
t-
=
��BP=OB-OP=5-5t=5-
��5=
��
��BP=OQ������B��Բ��P�ľ�����ڡ�P�İ뾶����B�ڡ�P�ϣ�
�����CP��AQ����ʱt=
���ҵ�B�ڡ�P�ϣ�
 �⣺��1����C��x��y����x��0��y��0����
�⣺��1����C��x��y����x��0��y��0������A��
| 25 |
| 6 |
��OA=
| 25 |
| 6 |
(3-
|
| 25 |
| 6 |
�߽֡���ABO����ֱ��OB���ۣ���A���ڵڶ������ڵĵ�C����
��OA=OC��AB=CB��
��
|
���
|
���C�������ǣ�-
| 7 |
| 6 |
��2����ͼ1������AC������B��BG��x���ڵ�G������C��CH��x���ڵ�H��
��A��
| 25 |
| 6 |
��OA=
| 25 |
| 6 |
��AG=
| 7 |
| 6 |
��AC=
| 20 |
| 3 |
��AE=
| 10 |
| 3 |
ͬ����OE=
| 5 |
| 2 |
�ٵ�0��t��
| 1 |
| 2 |
��OP=5t��
��PE=
| 5 |
| 2 |
��
| ||
| d |
| ||
|
��d=-
| 25 |
| 4 |
| 25 |
| 8 |
�ڵ�
| 1 |
| 2 |
| 25 |
| 4 |
| 25 |
| 8 |
��3����ͼ2������P��PK��AB�ڵ�K��
��CP��AQ��
���PCE=��QAE��
��AE=CE��AC��BO��
��PC=PA��
���PAE=��PCE=
| 1 |
| 2 |
���PAB=��QAE��
���PAE=��PAB��
��PE=PK��
��������ABCO����PBK=��OBF��
��sin��PBK=sin��OBF=
| OF |
| OB |
| PK |
| PB |
| 4 |
| 5 |
��OP=5t��OB=5��
��PE=
| 5 |
| 2 |
��
5t-
| ||
| 5-5t |
| 4 |
| 5 |
��ã�t=
| 13 |
| 18 |
�����CP��AQ����ʱt=
| 13 |
| 18 |
��
| 1 |
| 2 |
| 13 |
| 18 |
��t=
| 13 |
| 18 |
| 25 |
| 4 |
| 25 |
| 8 |
| 25 |
| 18 |
| 13 |
| 18 |
| 25 |
| 18 |
��BP=OQ������B��Բ��P�ľ�����ڡ�P�İ뾶����B�ڡ�P�ϣ�
�����CP��AQ����ʱt=
| 13 |
| 18 |
�����������ۺϿ����˷��۱任�����ɶ��������ε������Լ�����Բ��λ�ù�ϵ��֪ʶ�㣮ע�⣬���2��ʱ��Ҫ�������ۣ��Է�©�⣮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
 ��2012•������һģ����ͼ��һ���洬λ�ں���۲�վP�ı�ƫ��60�㷽���洬��A���뺣��۲�վP�ľ���Ϊ80 ����������Ϸ�����һ��ʱ�����λ�ں���۲�վP����ƫ��45�㷽���ϵ�B�������ʱ�洬���ڵ�B���뺣��۲�վP�ľ���Ϊ
��2012•������һģ����ͼ��һ���洬λ�ں���۲�վP�ı�ƫ��60�㷽���洬��A���뺣��۲�վP�ľ���Ϊ80 ����������Ϸ�����һ��ʱ�����λ�ں���۲�վP����ƫ��45�㷽���ϵ�B�������ʱ�洬���ڵ�B���뺣��۲�վP�ľ���Ϊ ��2012•������һģ����ͼ���³�С���ƻ�����դ��Χ��һ�����εij���ABCD��Ϊ�˷���泵����CD���Ͽ���һ��lm�����ţ���BC���Ͽ���һ��2m�����ţ��Ų�������դ�����ɵģ�����AB�߳�Ϊx��m����AD�߳�Ϊy��m������AB��AD��
��2012•������һģ����ͼ���³�С���ƻ�����դ��Χ��һ�����εij���ABCD��Ϊ�˷���泵����CD���Ͽ���һ��lm�����ţ���BC���Ͽ���һ��2m�����ţ��Ų�������դ�����ɵģ�����AB�߳�Ϊx��m����AD�߳�Ϊy��m������AB��AD��