题目内容
先阅读下列知识,然后解答下面两个问题:
含有一个未知数,并且未知数的最高次指数是2的方程,叫做一元二次方程,如:x2-2x+1=0.我们把它的一般形式记作:ax2+bx+c=0(a、b、c表示已知量,x是未知数,a≠0),它的解的情况是:
①当b2-4ac>0时,方程有两个不相等的解;
②当b2-4ac=0时,方程有两个相等的解(即一个解);
③当b2-4ac<0时,方程没有解;
(1)一元二次方程2x2-3x+1=0有几个解?为什么?
(2)当m取何值时,关于x的一元二次方程x2-2x+(m-1)=0没有解?
含有一个未知数,并且未知数的最高次指数是2的方程,叫做一元二次方程,如:x2-2x+1=0.我们把它的一般形式记作:ax2+bx+c=0(a、b、c表示已知量,x是未知数,a≠0),它的解的情况是:
①当b2-4ac>0时,方程有两个不相等的解;
②当b2-4ac=0时,方程有两个相等的解(即一个解);
③当b2-4ac<0时,方程没有解;
(1)一元二次方程2x2-3x+1=0有几个解?为什么?
(2)当m取何值时,关于x的一元二次方程x2-2x+(m-1)=0没有解?
分析:(1)先计算出△=(-3)2-4×2×1,得到△>0,然后根据△的意义判断根的情况;
(2)根据△的意义得到当△=(-2)2-4(m-1)<0时,方程没有解,然后解不等式即可.
(2)根据△的意义得到当△=(-2)2-4(m-1)<0时,方程没有解,然后解不等式即可.
解答:解:(1)∵△=(-3)2-4×2×1=1>0,
∴元二次方程2x2-3x+1=0有两个不相等的实数根;
(2)当△=(-2)2-4(m-1)<0时,方程没有解,
解不等式得m>2,
故当m>2时,关于x的一元二次方程x2-2x+(m-1)=0没有解.
∴元二次方程2x2-3x+1=0有两个不相等的实数根;
(2)当△=(-2)2-4(m-1)<0时,方程没有解,
解不等式得m>2,
故当m>2时,关于x的一元二次方程x2-2x+(m-1)=0没有解.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
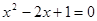 .
.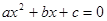 (a、b、c表示已知量,
(a、b、c表示已知量,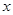 是未知数,a≠0),它的解的情况是:
是未知数,a≠0),它的解的情况是: 时,方程有两个不相等的解;
时,方程有两个不相等的解;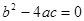 时,方程有两个相等的解(即一个解);
时,方程有两个相等的解(即一个解);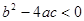 时,方程没有解;
时,方程没有解;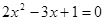 有几个解?为什么?
有几个解?为什么? 取何值时,关于
取何值时,关于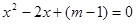 没有解?
没有解?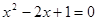 .
.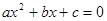 (a、b、c表示已知量,
(a、b、c表示已知量,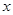 是未知数,a≠0),它的解的情况是:
是未知数,a≠0),它的解的情况是: 时,方程有两个不相等的解;
时,方程有两个不相等的解; 时,方程有两个相等的解(即一个解);
时,方程有两个相等的解(即一个解);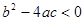 时,方程没有解;
时,方程没有解; 有几个解?为什么?
有几个解?为什么?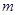 取何值时,关于
取何值时,关于 没有解?
没有解?