题目内容

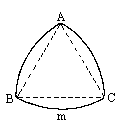
6、以等边△ABC的三个顶点为圆心的⊙A、⊙B与⊙C，若其中⊙A与⊙B相外切，⊙A与⊙C也外切，而⊙B与⊙C相外离，则⊙A的半径R_A与⊙B的半径R_B之间的大小关系是（　　）

A、R_A＞R_B

B、R_A=R_B

C、R_A＜R_B

D、以上都有可能

分析：首先知道两圆的几种位置关系，它们的圆心距与半径之间的关系，然后比较两圆半径的大小．

解答：解：∵⊙A与⊙B相外切，⊙A与⊙C也外切，
∴R_A+R_B=R_A+R_C，
∵⊙B与⊙C相外离，
∴R_B+R_C＜R_A+R_C，
∴R_A＞R_B．
故选A．

点评：本题主要考查圆与圆的位置关系，①外离，则d＞R+r；②外切，则d=R+r；③相交，则R-r＜d＜R+r；④内切，则d=R-r；⑤内含，则d＜R-r．

练习册系列答案

暑假作业二十一世纪出版社系列答案

相关题目

如图，分别以等边△ABC的三个顶点为圆心，边长a为半径作弧AB、弧BC、弧CA．你有办法求出弧AB、弧BC、弧CA所围成的图形(曲边三角形)的面积吗？若有，请你求出．

如图，某市三个城镇中心A，B，C恰好分别位于一个等边三角形的三个顶点处，在三个城镇中心之间铺设通信光缆，以城镇A为出发点设计了三种连接方案：

(1)AB＋BC；

(2)AD＋BC(D为BC的中点)；

(3)OA＋OB＋OC(O为△ABC三边的垂直平分线的交点)．要使铺设的光缆长度最短应选哪种方案？

以等边△ABC的三个顶点为圆心的⊙A、⊙B与⊙C，若其中⊙A与⊙B相外切，⊙A与⊙C也外切，而⊙B与⊙C相外离，则⊙A的半径R_A与⊙B的半径R_B之间的大小关系是

以等边△ABC的三个顶点为圆心的⊙A、⊙B与⊙C，若其中⊙A与⊙B相外切，⊙A与⊙C也外切，而⊙B与⊙C相外离，则⊙A的半径RA与⊙B的半径RB之间的大小关系是