Question

某校数学课外小组利用数轴为学校门口的一条马路设计植树方案如下：第k棵树种植在点x处，其中x=1，当k≥2时，x=x+T－T，T（a）表示非负实数a的整数部分，例如T（2.6）=2，T（0.2）=0。按此方案，第6棵树种植点x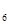为_____；第2011棵树种植点x为_____。

Answer 1

2；403

解析试题分析：由题意可知，数列x_n为1，2，3，4，5，1，2，3，4，5，1，2，3，4，5，…，由此入手能够得到第6棵树种植点x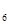和第2011棵树种植点x．
解：∵T－T组成的数列为1，0，0，0，0，1，0，0，0，0，1，0，0，0，0，1…，k=1，2，3，4，5，…
一一代入计算得数列x_n为1，2，3，4，5，1，2，3，4，5，1，2，3，4，5，…
即x_n的重复规律是x_5n+1=1，x_5n+2=2，x_5n+3=3，x_5n+4=4，x_5n=5．
∴第6棵树种植点x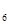为2，第2011棵树种植点x为403.
考点：找规律-数字的变化
点评：解答此类问题的关键是仔细分析所给数字的特征得到规律，再把得到的规律应用于解题.