题目内容
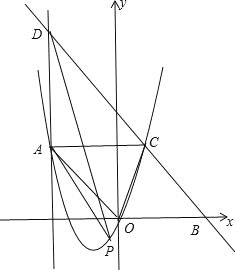
【题目】在平面直角坐标系xOy中,抛物线y=ax2+bx经过点A(﹣3,4),直线l与x轴相交于点B,与∠AOB的平分线相交于点C,直线l的解析式为y=kx﹣5k(k≠0),BC=OB.
(1)若点C在此抛物线上,求抛物线的解析式;
(2)在(1)的条件下,过点A作y轴的平行线,与直线l相交于点D,设P为抛物线上的一个动点,连接PA、PD,当![]() 时,求点P的坐标.
时,求点P的坐标.

【答案】(1)y=![]() x2+
x2+![]() x;(2)(﹣1,0)或(﹣5,
x;(2)(﹣1,0)或(﹣5,![]() )
)
【解析】
试题分析:(1)如图,先求出B点坐标,则可得到OA=OB=5,再证明AO∥CB,加上OB=BC=5,则可判断四边形AOBC为平行四边形,所以AC∥OB,AC=OB=5,于是得到C(2,4),然后利用待定系数法求抛物线解析式;
(2)如图,先确定直线l的解析式为y=﹣![]() x+
x+![]() ,再确定D点坐标,则可求出AD的长,设P(t,
,再确定D点坐标,则可求出AD的长,设P(t,![]() t2+
t2+![]() t),利用三角形面积公式和
t),利用三角形面积公式和![]() 得到
得到![]()
![]() |t+3|=
|t+3|=![]()
![]() 54,然后解绝对值方程求出t的值,从而可确定点P的坐标.
54,然后解绝对值方程求出t的值,从而可确定点P的坐标.
试题解析:(1)如图,A(﹣3,4),
∴OA=![]() =5,
=5,
当y=0时,kx﹣5k=0,解得x=5,则B(5,0),
∵BC=BO=5,
∴∠BOC=∠BCO,
∵OC平分∠AOB,
∴∠AOC=∠BOC,
∴∠AOC=∠BCO,
∴AO∥CB,
而OA=BC=5,
∴四边形AOBC为平行四边形,
∴AC∥OB,AC=OB=5,
∴C(2,4),
把A(﹣3,4),C(2,4)代入y=ax2+bx得![]() ,
,
解得a=![]() ,b=
,b=![]() ,
,
∴抛物线的解析式为y=![]() x2+
x2+![]() x;
x;
(2)如图,把C(2,4)代入y=kx﹣5k得2k﹣5k=4,解得k=﹣![]() ,
,
∴直线l的解析式为y=﹣![]() x+
x+![]() ,
,
当x=﹣2时,y=﹣![]() x+
x+![]() =
=![]() ,则D(﹣3,
,则D(﹣3,![]() ),
),
∴AD=![]() ﹣4=
﹣4=![]() ,
,
设P(t,![]() t2+
t2+![]() t),
t),
∵![]() ,
,
∴![]()
![]() |t+3|=
|t+3|=![]()
![]() 54,解得t=﹣1或t=﹣5,
54,解得t=﹣1或t=﹣5,
∴点P的坐标为(﹣1,0)或(﹣5,![]() ).
).