题目内容
【题目】△ABC中，∠BAC=90°，AB=AC，点D是BC的中点，把一个三角板的直角顶点放在点D处，将三角板绕点D旋转且使两条直角边分别交AB、AC于E、F .
（1）如图1，观察旋转过程，猜想线段AF与BE的数量关系并证明你的结论；
（2）如图2，若连接EF，试探索线段BE、EF、FC之间的数量关系，直接写出你的结论（不需证明）；
（3）如图3，若将“AB=AC，点D是BC的中点”改为：“∠B=30°，AD⊥BC于点D”，其余条件不变，探索（1）中结论是否成立？若不成立，请探索关于AF、BE的比值.
【答案】（1）证明见解析；（2）
；（3）（1）中结论不成立.
【解析】试题分析：（1）连接AD，利用等腰三角形中的三线合一，即可证得AD=BD=DC=
BC，∠ADB=∠ADC=90°，又由同角的余角相等，证得∠5=∠4，则可得△BDE≌△ADF，则AF=BE；
（2）由（1）可得AF=BE，AE=CF，又由勾股定理，即可得到；
（3）可证得有两角对应相等，所以可得△BDE∽△ADF，利用三角函数即可求得比值．
（1）如图，连接AD，
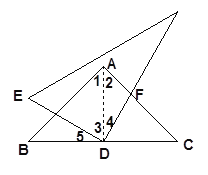
∵AB=AC，∠BAC=90°，点D是BC的中点
∴AD=BD=DC=BC，∠ADB=∠ADC=90°
∴∠B=∠C=∠1=∠2=45°
∴∠3+∠5==90°
∵∠3+∠4==90°
∴∠5=∠4
∵BD=AD
∴△BDE≌△ADF.
∴BE=AF；
（2）根据（1）可得BE=AF，
所以AB-BE=AC-AF，即AE=FC，
∵∠BAC=90°，
∴
，
∴
（3）（1）中的结论BE=AF不成立.
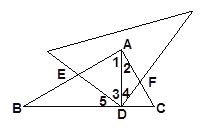
∵∠B=30°，AD⊥BC于点D，∠BAC=90°,
∴∠3+∠5==90°， ∠B+∠1==90°.
∵∠3+∠4==90°，∠1+∠2==90°
∴∠B="∠2" ， ∠5=∠4.
∴△BDE∽△ADF.
∴
.
