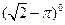题目内容
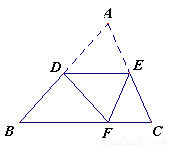
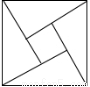
如图,D为AB的中点,点E在AC上,将△ABC沿DE折叠,使点A落在BC边上的点F处.
求证:EF=EC.
证明见解析.
【解析】
试题分析:根据折叠的性质得到DA=DF,AE=FE,∠ADE=∠FDE,根据等腰三角形性质得∠B=∠DFB,再根据三角形外角性质得到∠ADE+∠FDE=∠B+∠DFB,则∠ADE=∠B,所以DE∥BC,易得DE为△ABC的中位线,得到AE=EC,于是EF=EC.
试题解析:∵△ABC沿DE折叠,使点A落在BC边上的点F处,
∴DA=DF,AE=FE,∠ADE=∠FDE,
∴∠B=∠DFB,
∵∠ADF=∠B+∠DFB,即∠ADE+∠FDE=∠B+∠DFB,
∴∠ADE=∠B,
∴DE∥BC,
而D为AB的中点,
∴DE为△ABC的中位线,
∴AE=EC,
∴EF=EC.
考点: 翻折变换(折叠问题)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




 +
+