题目内容
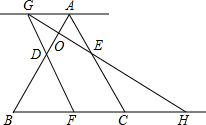 已知:如图,等边三角形ABC的边长为6,点D,E分别在边AB,AC上,且AD=AE=2.若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设点F运动的时间为t秒.当t>0时,直线FD与过点A且平行于BC的直线相交于点G,GE的延长线与BC的延长线相交于点H,AB与GH相交于点O.
已知:如图,等边三角形ABC的边长为6,点D,E分别在边AB,AC上,且AD=AE=2.若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设点F运动的时间为t秒.当t>0时,直线FD与过点A且平行于BC的直线相交于点G,GE的延长线与BC的延长线相交于点H,AB与GH相交于点O.(1)设△EGA的面积为S,写出S与t的函数关系式;
(2)当t为何值时,AB⊥GH.
分析:(1)由GA∥BC,可得△ADG∽△BDF,然后由相似三角形的对应边成比例,易得
=
,继而可求得AG的长,然后过点E作EK⊥AG于点K,由含30°角的直角三角形的性质,可求得EK的长,继而求得答案;
(2)首先连接DE,易得△ADE是等边三角形,然后若AB⊥HE,则AO=OD,∠AEO=∠OED,易得△AGE是等腰三角形,继而求得答案.
| AG |
| BF |
| AD |
| DB |
(2)首先连接DE,易得△ADE是等边三角形,然后若AB⊥HE,则AO=OD,∠AEO=∠OED,易得△AGE是等腰三角形,继而求得答案.
解答: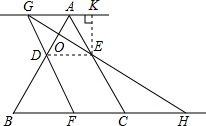 解:(1)∵GA∥BC,
解:(1)∵GA∥BC,
∴∠GAD=∠B,∠AGD=∠BFD,
∴△ADG∽△BDF,
∴
=
,
∵AB=6,AD=2,
∴DB=4,
∵BF=t,
∴
=
,
∴AG=
t,
过点E作EK⊥AG于点K,
∵∠BCA=60°,
∴∠CAK=60°,
∴∠AEK=30°,
∵AE=2,
∴AK=1,EK=
,
∴S=
AG•EK=
×
t×
=
t;
(2)连接DE,
∵AD=AE,
∵∠BAC=60°,
∴△ADE是等边三角形,
若AB⊥HE,则AO=OD,∠AEO=∠OED,
∵GA∥DE,
∴∠AGE=∠GED,
∴∠AGE=∠AEG,
∴AG=AE=2,
∴
t=2,
解得:t=4,
∴当t=4时,AB⊥GH.
 解:(1)∵GA∥BC,
解:(1)∵GA∥BC,∴∠GAD=∠B,∠AGD=∠BFD,
∴△ADG∽△BDF,
∴
| AG |
| BF |
| AD |
| DB |
∵AB=6,AD=2,
∴DB=4,
∵BF=t,
∴
| AG |
| t |
| 2 |
| 4 |
∴AG=
| 1 |
| 2 |
过点E作EK⊥AG于点K,
∵∠BCA=60°,
∴∠CAK=60°,
∴∠AEK=30°,
∵AE=2,
∴AK=1,EK=
| 3 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 4 |
(2)连接DE,
∵AD=AE,
∵∠BAC=60°,
∴△ADE是等边三角形,
若AB⊥HE,则AO=OD,∠AEO=∠OED,
∵GA∥DE,
∴∠AGE=∠GED,
∴∠AGE=∠AEG,
∴AG=AE=2,
∴
| 1 |
| 2 |
解得:t=4,
∴当t=4时,AB⊥GH.
点评:此题考查了相似三角形的判定与性质、等边三角形的判定与性质以及含30°角的直角三角形的性质.此题难度较大,注意掌握辅助线的作法,注意数形结合与方程思想的应用.

练习册系列答案
相关题目
 类似地你可以得到:“满足
类似地你可以得到:“满足

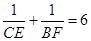 ,则等边三角
,则等边三角
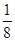 B.
B. 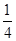 C.
C.
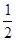 D.1
D.1