Question

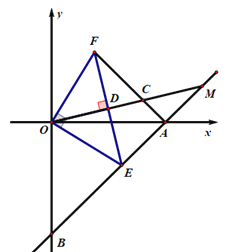
【题目】如图，直线AB与x轴交于点A（4，0），与y轴交于点B（0，－4），若点E在线段AB上，OE⊥OF，且OE＝OF，连接AF.

（1）猜想线段AF与BE之间的关系，并证明；

（2）过点O作OM⊥EF垂足为D,OM分别交AF、BA的延长线于点C、M若BE=，求CF的长.

Answer 1

【答案】(1) AF=BE，证明见解析 （2）CF=

【解析】

(1)由已知可得：∠FOE=∠AOB=90°，减去公共角∠AOE可得：∠FOA=∠EOB，又因为OE=OF,OA=OB,可证FOAEOB,即可得AF与BE相等.

（2）由(1)可得∠FAO=∠OBA=∠OAB=45°,可得∠FAE=90°，由A,B坐标可求得AB=4，又AF=BE=，得AE的长.连接EC，根据等腰三角形的“三线合一”可得OM垂直平分EF，则FC=EC，设FC=EC=x，则AC=，在直角三角形AEC中，根据勾股定理列出方程，代入数值即可求得CF的长.

(1) AF=BE，证明：

∵直线AB与x轴交于点A（4，0），与y轴交于点B（0，－4）

∴OA=OB=4

∵OE⊥OF

∴∠FOE=∠AOB=90°

∴∠FOE-∠AOE=∠AOB-∠AOE

即∠FOA=∠EOB

在FOA和EOB中

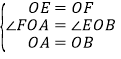
∴FOAEOB（SAS）

∴AF=BE

（2）连接EC.

∵OA=OB=4，∠AOB=90°

∴∠OBA=∠OAB=45°，AB=4

由（1）得：FOAEOB

∴∠FAO=∠OBA=∠OAB=45°，AF=BE=

∴∠FAE=90°，AE=

∵OE=OF， OM⊥EF

∴OM垂直平分EF

∴FC=EC

设FC=EC=x，则AC=

根据勾股定理得：

解得

∴CF=