题目内容
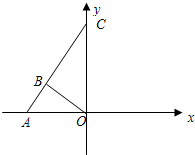
如图,Rt△ABO在直角坐标系中,∠ABO=90°,点A(-25,0),∠A的正切值为 ,直线AB与y轴交于点C.
,直线AB与y轴交于点C.(1)求点B的坐标;
(2)将△ABO绕点O顺时针旋转,使点B落在x轴正半轴上的B′处.试在直角坐标系中画出旋转后的△A′B′O,并写出点A′的坐标;
(3)在直线OA′上是否存在点D,使△COD与△AOB相似?若存在,求出点D的坐标;若不存在,请说明理由.

【答案】分析:(1)过点B作BH⊥AO于H,由tgA= ,设BH=4k,AH=3k,则AB=5k,在Rt△ABO中由tgA=
,设BH=4k,AH=3k,则AB=5k,在Rt△ABO中由tgA= ,AO=25即可求出AB、BH、AH及OH的长,进而可得出B点坐标;
,AO=25即可求出AB、BH、AH及OH的长,进而可得出B点坐标;
(2)由图形旋转的性质画出△A′B′C′,由OB′A′B′的长即可求出A′点的坐标;
(3)在Rt△AOC中,由AO=25,tgA= 可求出OC的长,设OA′的解析式为y=kx,由A′点的坐标即可求出k的值,由图形旋转的性质可得出在直线OA′上存在点D符合条件,设点D的坐标为(x,
可求出OC的长,设OA′的解析式为y=kx,由A′点的坐标即可求出k的值,由图形旋转的性质可得出在直线OA′上存在点D符合条件,设点D的坐标为(x, x),则OD=
x),则OD= ,分别根据△COD∽△AOB、△COD∽△AOB求出x的值,进而可得出D点坐标.
,分别根据△COD∽△AOB、△COD∽△AOB求出x的值,进而可得出D点坐标.
解答: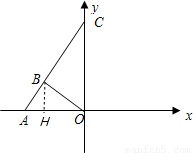 解:(1)过点B作BH⊥AO于H,由tgA=
解:(1)过点B作BH⊥AO于H,由tgA= ,设BH=4k,AH=3k,则AB=5k
,设BH=4k,AH=3k,则AB=5k
在Rt△ABO中,
∵tgA= ,AO=25,
,AO=25,
∴AB=15(1分)
∴k=3,
∴BH=12(1分),AH=9,
∴OH=16(1分)
∴B(-16,12)(1分)
(2)正确画图(2分)
A′(20,15)(2分)
(3)在Rt△AOC中,AO=25,tgA= ,
,
∴OC=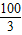 (1分)
(1分)
设OA′的解析式为y=kx,则15=20k,则k= ,
,
∴y= x(1分)
x(1分)
∵△ABO旋转至△A′B′O,
∴∠AOB=∠A′OB′,
∵∠AOB+∠A=90°,∠COA′+∠A′OB′=90°,
∴∠A=∠COA′
∴在直线OA′上存在点D符合条件,设点D的坐标为(x, x),则OD=
x),则OD=
1°当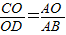 即
即 ,也即x=16时,△COD与△AOB相似,
,也即x=16时,△COD与△AOB相似,
此时D(16,12)(2分)
2°当 即
即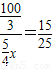 ,也即x=
,也即x= 时,△COD与△AOB相似,
时,△COD与△AOB相似,
此时D(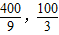 )(2分)
)(2分)
点评:本题考查的是相似三角形的判定与性质,涉及到坐标与图形的性质、图形旋转的性质及解直角三角形,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
 ,设BH=4k,AH=3k,则AB=5k,在Rt△ABO中由tgA=
,设BH=4k,AH=3k,则AB=5k,在Rt△ABO中由tgA= ,AO=25即可求出AB、BH、AH及OH的长,进而可得出B点坐标;
,AO=25即可求出AB、BH、AH及OH的长,进而可得出B点坐标;(2)由图形旋转的性质画出△A′B′C′,由OB′A′B′的长即可求出A′点的坐标;
(3)在Rt△AOC中,由AO=25,tgA=
 可求出OC的长,设OA′的解析式为y=kx,由A′点的坐标即可求出k的值,由图形旋转的性质可得出在直线OA′上存在点D符合条件,设点D的坐标为(x,
可求出OC的长,设OA′的解析式为y=kx,由A′点的坐标即可求出k的值,由图形旋转的性质可得出在直线OA′上存在点D符合条件,设点D的坐标为(x, x),则OD=
x),则OD= ,分别根据△COD∽△AOB、△COD∽△AOB求出x的值,进而可得出D点坐标.
,分别根据△COD∽△AOB、△COD∽△AOB求出x的值,进而可得出D点坐标.解答:
 解:(1)过点B作BH⊥AO于H,由tgA=
解:(1)过点B作BH⊥AO于H,由tgA= ,设BH=4k,AH=3k,则AB=5k
,设BH=4k,AH=3k,则AB=5k在Rt△ABO中,
∵tgA=
 ,AO=25,
,AO=25,∴AB=15(1分)
∴k=3,
∴BH=12(1分),AH=9,
∴OH=16(1分)

∴B(-16,12)(1分)
(2)正确画图(2分)
A′(20,15)(2分)
(3)在Rt△AOC中,AO=25,tgA=
 ,
,∴OC=
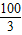 (1分)
(1分)设OA′的解析式为y=kx,则15=20k,则k=
 ,
,∴y=
 x(1分)
x(1分)∵△ABO旋转至△A′B′O,
∴∠AOB=∠A′OB′,
∵∠AOB+∠A=90°,∠COA′+∠A′OB′=90°,
∴∠A=∠COA′
∴在直线OA′上存在点D符合条件,设点D的坐标为(x,
 x),则OD=
x),则OD=
1°当
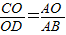 即
即 ,也即x=16时,△COD与△AOB相似,
,也即x=16时,△COD与△AOB相似,此时D(16,12)(2分)
2°当
 即
即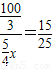 ,也即x=
,也即x= 时,△COD与△AOB相似,
时,△COD与△AOB相似,此时D(
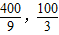 )(2分)
)(2分)点评:本题考查的是相似三角形的判定与性质,涉及到坐标与图形的性质、图形旋转的性质及解直角三角形,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
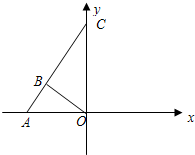 直线AB与y轴交于点C.
直线AB与y轴交于点C.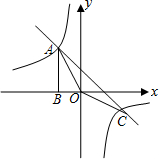 如图,Rt△ABO的顶点A是反比例函数y=
如图,Rt△ABO的顶点A是反比例函数y=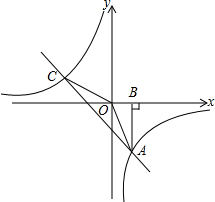 如图,Rt△ABO的顶点A是双曲线y=
如图,Rt△ABO的顶点A是双曲线y= ,
, 直线AB与y轴交于点C.
直线AB与y轴交于点C.