题目内容
(2007•天门)如图,直线y=- x+1与x轴交于点A,与y轴交于点B,以AB为边在第一象限内作正△ABC.
x+1与x轴交于点A,与y轴交于点B,以AB为边在第一象限内作正△ABC.(1)求点C的坐标;
(2)把△ABO沿直线AC翻折,点B落在点D处,点D是否在经过点C的反比例函数的图象上?说明理由;
(3)连接CD,判断四边形ABCD是什么四边形?说明理由.

【答案】分析:(1)用特殊角的三角函数值及等边三角形的性质求出C的坐标;
(2)根据反比例函数的解析式,求出点D在过点C的反比例函数的图象上;
(3)根据菱形的性质判断出四边形ABCD是菱形.
解答:解:(1)∵直线y=- x+1与x轴交于点A(
x+1与x轴交于点A(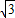 ,0),与y轴相交于点B(0,1),
,0),与y轴相交于点B(0,1),
∴tan∠BAO= =
= ,
,
∴∠BAO=30°,
∵△ABC为正三角形,
∴∠BAC=60°,
∴∠CAO=90°,
∵AB=AC=2,
∴点C的坐标为( ,2);
,2);
(2)过C的反比例函数解析式为y= ,
,
点D与B(0,1)关于直线AC:x= 对称,
对称,
∴点D坐标为( ,1),
,1),
∴点D在过点C的反比例函数的图象上;
(3)四边形ABCD是菱形.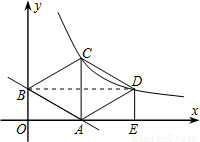
连接BD,点B与D关于直线AC对称,
∴BD⊥AC,
∵△ABC是正三角形,
∴A、C关于BD对称,
故ABCD的对角线AC与BD互相垂直平分,
∴四边形ABCD是菱形.
点评:综合了特殊角的三角函数值,反比例函数的解析式,菱形及等边三角形的性质,是一道综合性较好的题目.
(2)根据反比例函数的解析式,求出点D在过点C的反比例函数的图象上;
(3)根据菱形的性质判断出四边形ABCD是菱形.
解答:解:(1)∵直线y=-
 x+1与x轴交于点A(
x+1与x轴交于点A(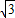 ,0),与y轴相交于点B(0,1),
,0),与y轴相交于点B(0,1),∴tan∠BAO=
 =
= ,
,∴∠BAO=30°,
∵△ABC为正三角形,
∴∠BAC=60°,
∴∠CAO=90°,
∵AB=AC=2,
∴点C的坐标为(
 ,2);
,2);(2)过C的反比例函数解析式为y=
 ,
,点D与B(0,1)关于直线AC:x=
 对称,
对称,∴点D坐标为(
 ,1),
,1),∴点D在过点C的反比例函数的图象上;
(3)四边形ABCD是菱形.

连接BD,点B与D关于直线AC对称,
∴BD⊥AC,
∵△ABC是正三角形,
∴A、C关于BD对称,
故ABCD的对角线AC与BD互相垂直平分,
∴四边形ABCD是菱形.
点评:综合了特殊角的三角函数值,反比例函数的解析式,菱形及等边三角形的性质,是一道综合性较好的题目.

练习册系列答案
相关题目
 x+1与x轴交于点A,与y轴交于点B,以AB为边在第一象限内作正△ABC.
x+1与x轴交于点A,与y轴交于点B,以AB为边在第一象限内作正△ABC.
 x+1与x轴交于点A,与y轴交于点B,以AB为边在第一象限内作正△ABC.
x+1与x轴交于点A,与y轴交于点B,以AB为边在第一象限内作正△ABC.
 x+1与x轴交于点A,与y轴交于点B,以AB为边在第一象限内作正△ABC.
x+1与x轴交于点A,与y轴交于点B,以AB为边在第一象限内作正△ABC.
 x+1与x轴交于点A,与y轴交于点B,以AB为边在第一象限内作正△ABC.
x+1与x轴交于点A,与y轴交于点B,以AB为边在第一象限内作正△ABC.