题目内容
【题目】某采摘农场计划种植A,B两种草莓共6亩,根据表格信息,解答下列问题:
项目 品种 | A | B |
年亩产(单位:千克) | 1200 | 2000 |
采摘价格 (单位:元/千克) | 60 | 40 |
(1)若该农场每年草莓全部被采摘的总收入为460000元,那么A、B两种草莓各种多少亩?
(2)若要求种植A种草莓的亩数不少于种植B种草莓的一半,那么种植A种草莓多少亩时,可使该农场每年草莓全部被采摘的总收入最多?并求出最多总收入.
【答案】(1) A种草莓种植2.5亩,B种草莓种植3.5亩;(2) 种植A种草莓的亩数不少于种植B种草莓的一半,那么种植A种草莓2亩时,可使农场每年草莓全部被采摘的总收入最多, 最多为464000元.
【解析】试题分析:(1)根据等量关系:总收入=A地的亩数×年亩产量×采摘价格+B地的亩数×年亩产量×采摘价格,列方程求解.
(2)这是一道只有一个函数关系式的求最值问题,根据题意确定自变量的取值范围,由函数y随x的变化求出最大利润.
试题解析:解:(1)设该农场种植A种草莓x亩,B种草莓(6﹣x)亩,
依题意,得:60×1200x+40×2000(6﹣x)=460000,
解得:x=2.5,
则6﹣x=3.5,
答:A种草莓种植2.5亩,B种草莓种植3.5亩.
(2)由x≥![]() (6﹣x),
(6﹣x),
解得x≥2
设农场每年草莓全部被采摘的收入为y元,则:
y=60×1200x+40×2000(6﹣x)=﹣8000x+480000,
∴当x=2时,y有最大值为464000,
答:种植A种草莓的亩数不少于种植B种草莓的一半,那么种植A种草莓2亩时,可使农场每年草莓全部被采摘的总收入最多.

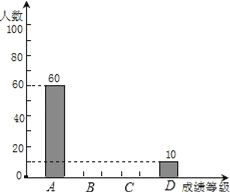
【题目】为了解某县2016年初中毕业生的实验考查成绩等级的分布情况,随机抽取了该县若干名学生的实验考查成绩进行统计分析,并根据抽取的成绩绘制了如下的统计图表:
成绩等级 | A | B | C | D |
人数 | 60 | x | y | 10 |
百分比 | 30% | 50% | 15% | m |
请根据以上统计图表提供的信息,解答下列问题:
(1)本次抽查的学生有 名;
(2)表中x,y和m所表示的数分别为:x= ,y= ,m= ;
(3)请补全条形统计图;
(4)根据抽样调查结果,请你估计2016年该县5400名初中毕业生实验考查成绩为D类的学生人数.