题目内容
已知一次函数y=ax+b(a、b是常数),x与y的部分对应值如下表:
不等式ax+b>0的解集是
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 6 | 4 | 2 | 0 | -2 | -4 |
x<1
根据不等式ax+b>0的解集为函数y=ax+b中y>0时自变量x的取值范围,由图表可知,y随x的增大而减小,因此x<1时,函数值y>0,即不等式ax+b>0的解为x<1.
解答:图表可得:当x=1时,y=0,
∴方程ax+b=0的解是x=1,y随x的增大而减小,
∴不等式ax+b>0的解是:x<1,
故答案为:x<1.
解答:图表可得:当x=1时,y=0,
∴方程ax+b=0的解是x=1,y随x的增大而减小,
∴不等式ax+b>0的解是:x<1,
故答案为:x<1.

练习册系列答案
相关题目
 的解都是负数,化简
的解都是负数,化简 。
。 的负整数解是 。
的负整数解是 。
 ,并求它的整数解.
,并求它的整数解.



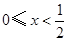

 的解在数轴上表示为( ▲ )
的解在数轴上表示为( ▲ )