题目内容
【题目】如图,双曲线y=![]() (x>0)经过△OAB的顶点A和OB的中点C.AB∥x轴,点A的坐标为(4,6),连接AC交x轴于D.连接BD.
(x>0)经过△OAB的顶点A和OB的中点C.AB∥x轴,点A的坐标为(4,6),连接AC交x轴于D.连接BD.
(1)确定k的值;
(2)求直线AC的解析式;
(3)判断四边形OABD的形状,并说明理由;
(4)求△OAC的面积.

【答案】(1)-![]() (2)直线AC解析式为y=-
(2)直线AC解析式为y=-![]() x+9;(3)四边形OABC为平行四边形,理由见解析;(4)18.
x+9;(3)四边形OABC为平行四边形,理由见解析;(4)18.
【解析】
试题分析:(1)把A的坐标代入反比例解析式求出k的值即可;
(2)由AB与x轴平行,且A纵坐标为6,得到B纵坐标为6,再由C为OB中点,确定出C纵坐标为3,代入反比例解析式确定出C坐标,利用待定系数法确定出直线AC解析式即可;
(3)四边形OABC为平行四边形,理由为:由C的坐标确定出B的坐标,进而确定出AB的长,由直线AC与x轴的交点为D,确定出D坐标,得出OD的长,由AB与OD平行且相等,得到四边形OABC为平行四边形;
(4)由四边形OABC为平行四边形,得到对角线互相平分,得到三角形AOC面积为平行四边形面积的四分之一,求出即可.
试题解析:(1)将A(4,6)代入解析式y=![]() 得:k=24;
得:k=24;
(2)∵AB∥x轴,B的纵坐标是6,C为OB中点,
∴把y=3代入反比例解析式得:x=8,即C坐标为(8,3),
设直线AC的解析式为y=kx+b,
将A(4,6)与C(8,3)代入得:
![]() ,
,
解得: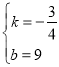 ,
,
则直线AC解析式为y=-![]() x+9;
x+9;
(3)四边形OABC为平行四边形,理由为:
∵点C的坐标为(8,3),
∴B的坐标为(16,6),即AB=12,
把y=0代入y=-![]() x+9中得:x=12,即D(12,0),
x+9中得:x=12,即D(12,0),
∴OD=12,
∴AB=OD,
∵AB∥OD,
∴四边形OABC为平行四边形;
(4)∵S四边形OABC=12×6=72,
∴S△OAC=![]() S四边形OABC=18.
S四边形OABC=18.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案