题目内容
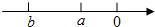 实数a,b在数轴上的对应点如图所示,化简
实数a,b在数轴上的对应点如图所示,化简| a2-4ab+4b2 |
分析:根据数轴上点的坐标特点,判断出可知b<a<0,且|b|>|a|,所以a-2b>0,a+b<0,再把二次根式化简即可.
解答:解:根据数轴可知b<a<0,且|b|>|a|,所以a-2b>0,a+b<0,
∴
+|a+b|=
-(a+b)
=a-2b-a-b=-3b.
∴
| a2-4ab+4b2 |
| (a-2b)2 |
=a-2b-a-b=-3b.
点评:本题主要考查了绝对值的意义和根据二次根式的意义化简.
二次根式
规律总结:当a≥0时,
=a;当a<0时,
=-a.
解题关键是先判断所求的代数式的正负性.
二次根式
| a2 |
| a2 |
| a2 |
解题关键是先判断所求的代数式的正负性.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
实数a,b在数轴上的位置,如图所示,那么化简
-|a+b|的结果是( )

| a2 |

| A、2a+b | B、b |
| C、-b | D、-2a+b |

 14、实数a、b在数轴上的位置如图所示:
14、实数a、b在数轴上的位置如图所示: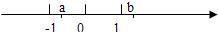
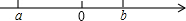 已知实数a,b在数轴上的对应点如图所示,化简:a-b+|a+b|得( )
已知实数a,b在数轴上的对应点如图所示,化简:a-b+|a+b|得( )