题目内容
【题目】如图,在边长为1的小正方形组成的网格中,△ABC和△DEF的顶点都在格点上,P1、P2、P3、P4、P5是△DEF边上的5个格点,请按要求完成下列各题:
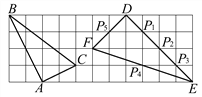
(1)试证明△ABC为直角三角形;
(2)判断△ABC和△DEF是否相似,并说明理由;
(3)直接写出一个与△ABC相似的三角形,使它的三个顶点为P1、P2、P3、P4、P5中的三个格点.
【答案】(1)证明见解析(2)证明见解析(3)△P2P4P5
【解析】试题分析:(1)运用勾股定理可以得到各边的长,通过勾股定理的逆定理来证明是直角三角形.
(2)根据勾股定理求出△ABC和△DEF的各边长,然后根据“三边对应成比例的两个三角形相似”说明即可;
(3)根据△ABC的三边关系,求出点P2,P4,P5所形成三角形的三边长,根据“三边对应成比例的两个三角形相似”解答即可,
解:(1)根据勾股定理,
得AB=![]() ,AC=
,AC=![]() ,BC=
,BC=![]() ;
;
∴AB2+AC2=BC2,
∴△ABC 为直角三角形
(2)△ABC和△DEF相似.理由如下:
∵AB=![]() ,AC=
,AC=![]() ,BC=5,
,BC=5,
DE=![]() ,DF=
,DF=![]() ,EF=
,EF=![]() .
.
∴![]() ,
,
∴△ABC∽△DEF
(3连接P2P5,P2P4,P4P5.

∵P2P5=![]() ,P2P4=
,P2P4=![]() ,P4P5=
,P4P5=![]() ,AB=
,AB=![]() ,AC=
,AC=![]() ,BC=5,
,BC=5,
∴![]() ,
,
∴△ABC∽△P4P5P2.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目