题目内容
若x是不为0的有理数,已知M=(x2+2x+1)(x2-2x+1),N=(x2+x+1)(x2-x+1),则M与N的大小是
- A.M>N
- B.M<N
- C.M=N
- D.无法确定
B
分析:运用乘法公式,在化简M、N的基础上,作差比较它们的大小即可.
解答:由M=(x2+2x+1)(x2-2x+1),
=x4-2x2+1,
N=(x2+x+1)(x2-x+1),
=x4+x2+1,
∴M-N=x4-2x2+1-(x4+x2+1),
=-3x2,
∵x是不为0的有理数,
∴-3x2<0,
即M<N.
故选B.
点评:本题考查了完全平方公式,属于基础题,关键是化简M,N后进行作差比较大小.
分析:运用乘法公式,在化简M、N的基础上,作差比较它们的大小即可.
解答:由M=(x2+2x+1)(x2-2x+1),
=x4-2x2+1,
N=(x2+x+1)(x2-x+1),
=x4+x2+1,
∴M-N=x4-2x2+1-(x4+x2+1),
=-3x2,
∵x是不为0的有理数,
∴-3x2<0,
即M<N.
故选B.
点评:本题考查了完全平方公式,属于基础题,关键是化简M,N后进行作差比较大小.

练习册系列答案
相关题目
 称为a的差倒数.如:2的差倒数是
称为a的差倒数.如:2的差倒数是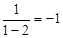 ,
,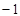 的差倒数是
的差倒数是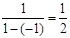 .已知
.已知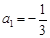 ,
,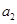 是
是 的差倒数,
的差倒数,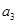 是
是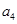 是
是 的值
的值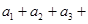 ……
…… 的值
的值