题目内容
抛物线
 过点
过点 ,顶点为M点.
,顶点为M点.

(1)求该抛物线的解析式;
(2)试判断抛物线上是否存在一点P,使∠POM=90˚.若不存在,说明理由;若存在,求出P点的坐标;
(3)试判断抛物线上是否存在一点K,使∠OMK=90˚,说明理由.
(1)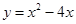 ;(2)
;(2)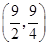 ;(3)存在.
;(3)存在.
【解析】
试题分析:(1)将A(1,-3),B(3,-3),C(-1,5)三点坐标代入y=ax2+bx+c中,列方程组求a、b、c的值,得出抛物线解析式;
(2)抛物线上存在一点P,使∠POM=90˚.设(a,a2-4a),过P点作PE⊥y轴,垂足为E;过M点作MF⊥y轴,垂足为F,利用互余关系证明Rt△OEP∽Rt△MFO,利用相似比求a即可;
(3)抛物线上必存在一点K,使∠OMK=90˚.过顶点M作MN⊥OM,交y轴于点N,在Rt△OMN中,利用互余关系证明△OFM∽△MFN,利用相似比求N点坐标,再求直线MN解析式,将直线MN解析式与抛物线解析式联立,可求K点坐标.
(1)根据题意,得
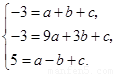
解得 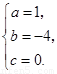
∴ 抛物线的解析式为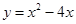 .
.
(2)抛物线上存在一点P,使∠POM=90˚.
x=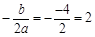 ,
,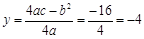 .
.
∴ 顶点M的坐标为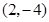 .
.
设抛物线上存在一点P,满足OP⊥OM,其坐标为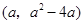 .
.
过P点作PE⊥y轴,垂足为E;过M点作MF⊥y轴,垂足为F.
则 ∠POE+∠MOF=90˚,∠POE+∠EPO=90˚.
∴ ∠EPO=∠FOM.
∵ ∠OEP=∠MFO=90˚,
∴ Rt△OEP∽Rt△MFO.
∴ OE∶MF=EP∶OF.
即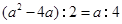 .
.
解,得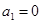 (舍去),
(舍去),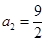 .
.
∴ P点的坐标为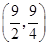 .
.
(3)

过顶点M作MN⊥OM,交y轴于点N.则 ∠FMN+∠OMF=90˚.
∵ ∠MOF+∠OMF=90˚,
∴ ∠MOF=∠FMN.
又∵ ∠OFM=∠MFN=90˚,
∴ △OFM∽△MFN.
∴ OF∶MF=MF∶FN. 即 4∶2=2∶FN.∴ FN=1.
∴ 点N的坐标为(0,-5).
设过点M,N的直线的解析式为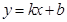 .
.
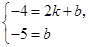 解,得
解,得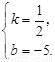 直线的解析式为
直线的解析式为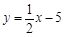 .
.
∴ 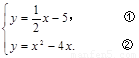 把①代入②,得
把①代入②,得 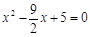 .
.
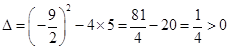 .
.
∴ 直线MN与抛物线有两个交点(其中一点为顶点M).
∴ 抛物线上必存在一点K,使∠OMK=90˚.
考点:本题考查了二次函数的综合运用
点评:解答本题的关键关键是通过已知三点求抛物线解析式,根据垂直关系证明三角形相似,得出线段长及点的坐标,利用直线解析式及抛物线解析式求满足条件的点的坐标.

 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案 已知一抛物线过点O(0,0),A(6,0),B(4,3),
已知一抛物线过点O(0,0),A(6,0),B(4,3),
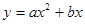 过点
过点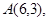 且对称轴为直线
且对称轴为直线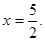 点B为直线OA下方的抛物线上一动点,点B的横坐标为m.
点B为直线OA下方的抛物线上一动点,点B的横坐标为m.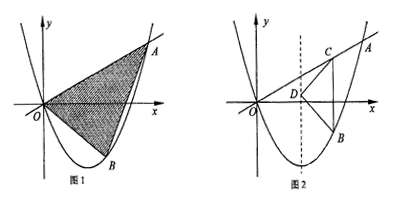
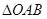 的面积为S.求S关于m的函数关系式,并求出S的最大值.
的面积为S.求S关于m的函数关系式,并求出S的最大值.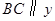 轴,交线段OA于点C,在抛物线的对称轴上是否存在点D,使
轴,交线段OA于点C,在抛物线的对称轴上是否存在点D,使 是以D为直角顶点的等腰直角三角形?若存在,求出所有符合条件的点B的坐标,若不存在,请说明理由.
是以D为直角顶点的等腰直角三角形?若存在,求出所有符合条件的点B的坐标,若不存在,请说明理由.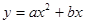 过点
过点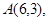 且对称轴为直线
且对称轴为直线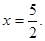 点B为直线OA下方的抛物线上一动点,点B的横坐标为m.
点B为直线OA下方的抛物线上一动点,点B的横坐标为m.
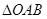 的面积为S.求S关于m的函数关系式,并求出S的最大值.
的面积为S.求S关于m的函数关系式,并求出S的最大值.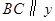 轴,交线段OA于点C,在抛物线的对称轴上是否存在点D,使
轴,交线段OA于点C,在抛物线的对称轴上是否存在点D,使 是以D为直角顶点的等腰直角三角形?若存在,求出所有符合条件的点B的坐标,若不存在,请说明理由.
是以D为直角顶点的等腰直角三角形?若存在,求出所有符合条件的点B的坐标,若不存在,请说明理由.