题目内容
 如图,一艘轮船在40海里/时的速度由西向东航行,上午8时到达A处,测得灯塔P在北偏东60°方向上;10时到达B处,测得灯塔P在北偏东30°方向上.当轮船到达灯塔P的正南时,轮船距灯塔P多远?
如图,一艘轮船在40海里/时的速度由西向东航行,上午8时到达A处,测得灯塔P在北偏东60°方向上;10时到达B处,测得灯塔P在北偏东30°方向上.当轮船到达灯塔P的正南时,轮船距灯塔P多远?
分析:过P作PC⊥AB,利用路程公式求AB,由等腰三角形,得AB=BP,由直角三角形性质得出BC与PB的关系.
解答:解:由已知条件,得∠PAB=30°,∠PBC=60°,过P作PC⊥AB,
在Rt△PBC中,∠PBC=60°,则∠BPC=30°,
∴BC=
PB,PC=
.
在Rt△APC中,∠PAB=30°,则∠APC=60°,
∴∠APB=30°.
∴∠APB=∠PAB.
∴PB=AB=(10-8)×40=80(海里).
∴BC=
PB=40(海里).
∴PC=
=40
(海里).
答:轮船到达灯塔P的正南方向时,距灯塔P40海里.
在Rt△PBC中,∠PBC=60°,则∠BPC=30°,
∴BC=
| 1 |
| 2 |
| PB2-BC2 |
在Rt△APC中,∠PAB=30°,则∠APC=60°,
∴∠APB=30°.
∴∠APB=∠PAB.
∴PB=AB=(10-8)×40=80(海里).
∴BC=
| 1 |
| 2 |
∴PC=
| 802-402 |
| 3 |
答:轮船到达灯塔P的正南方向时,距灯塔P40海里.
点评:解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
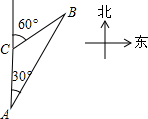 如图,一艘轮船以40海里/时的速度在海面上航行,当它行驶到A处时,发现它的北偏东30°方向有一灯塔B.轮船继续向北航行2小时后到达C处,发现灯塔B在它的北偏东60°方向.若轮船继续向北航行,那么当再过多长时间时轮船离灯塔最近?( )
如图,一艘轮船以40海里/时的速度在海面上航行,当它行驶到A处时,发现它的北偏东30°方向有一灯塔B.轮船继续向北航行2小时后到达C处,发现灯塔B在它的北偏东60°方向.若轮船继续向北航行,那么当再过多长时间时轮船离灯塔最近?( )
 小时 C.2小时 D.
小时 C.2小时 D. 小时
小时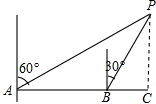 如图,一艘轮船在40海里/时的速度由西向东航行,上午8时到达A处,测得灯塔P在北偏东60°方向上;10时到达B处,测得灯塔P在北偏东30°方向上.当轮船到达灯塔P的正南时,轮船距灯塔P多远?
如图,一艘轮船在40海里/时的速度由西向东航行,上午8时到达A处,测得灯塔P在北偏东60°方向上;10时到达B处,测得灯塔P在北偏东30°方向上.当轮船到达灯塔P的正南时,轮船距灯塔P多远?