题目内容
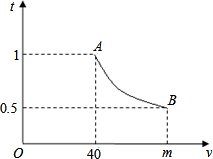
汽车匀速行驶在相距S千米的甲、乙两地之间,下图是行驶时间t(h)与行驶速度v(km/h )函数图象的一部分.
)函数图象的一部分.
(1)行驶时间t(h)与行驶速度v(km/h)之间的函数关系是:
(2)若该函数图象的两个端点为A(40,1)和B(m,0.5).求这个函数的解析式和m的值;
(3)若规定在该段公路上汽车的行驶速度不得超过50km/h,则汽车通过该路段最少需要多少时间?
 )函数图象的一部分.
)函数图象的一部分.(1)行驶时间t(h)与行驶速度v(km/h)之间的函数关系是:
t=
| 40 |
| v |
t=
.| 40 |
| v |
(2)若该函数图象的两个端点为A(40,1)和B(m,0.5).求这个函数的解析式和m的值;
(3)若规定在该段公路上汽车的行驶速度不得超过50km/h,则汽车通过该路段最少需要多少时间?
分析:(1)将点A(40,1)代入t=
,求得k,即可得出行驶时间t(h)与行驶速度v(km/h)之间的函数关系;
(2)利用(1)得出函数解析式,把点B代入求出的解析式中,求得m的值;
(2)求出v=50时的t值,汽车所用时间应大于等于这个值.
| k |
| v |
(2)利用(1)得出函数解析式,把点B代入求出的解析式中,求得m的值;
(2)求出v=50时的t值,汽车所用时间应大于等于这个值.
解答:解:(1)把(40,1)代入t=
,得k=40,
∴行驶时间t(h)与行驶速度v(km/h)之间的函数关系是:t=
,
故答案为:t=
.
(2)由(1)得出:函数的解析式为:t=
,
把(m,0.5)代入t=
,
0.5=
,
解得:m=80;
(3)把v=50代入t=
,得t=0.8,
答:汽车通过该路段最少需要0.8小时.
| k |
| v |
∴行驶时间t(h)与行驶速度v(km/h)之间的函数关系是:t=
| 40 |
| v |
故答案为:t=
| 40 |
| v |
(2)由(1)得出:函数的解析式为:t=
| 40 |
| v |
把(m,0.5)代入t=
| 40 |
| v |
0.5=
| 40 |
| m |
解得:m=80;
(3)把v=50代入t=
| 40 |
| v |
答:汽车通过该路段最少需要0.8小时.
点评:此题主要考查了反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.

练习册系列答案
相关题目
 A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入(城区与入口的距离忽略不计),并始终在高速公路上正常行驶.甲车驶往B城,乙车驶往A城,已知甲车以90千米/时的速度匀速行驶.两车之间的距离s(千米)与行驶时间x(小时)之间的关系如图.
A、B两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入(城区与入口的距离忽略不计),并始终在高速公路上正常行驶.甲车驶往B城,乙车驶往A城,已知甲车以90千米/时的速度匀速行驶.两车之间的距离s(千米)与行驶时间x(小时)之间的关系如图.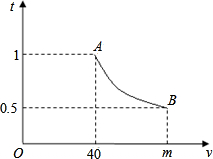 )函数图象的一部分.
)函数图象的一部分.