题目内容
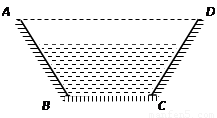
 如图是一个等腰梯形,若在该梯形中添加一条线段,可把这个梯形分成一个平行四边形和一个三角形,则这个三角形一定是
如图是一个等腰梯形,若在该梯形中添加一条线段,可把这个梯形分成一个平行四边形和一个三角形,则这个三角形一定是
- A.等边三角形
- B.等腰三角形
- C.直角三角形
- D.等腰直角三角形
B
分析:过点D作DE∥AB,可得出四边形ABED是平行四边形,△DCE是等腰三角形,故可得出结论.
解答: 解:过点D作DE∥AB,
解:过点D作DE∥AB,
∵四边形ABCD是等腰梯形,
∴AD∥BC,
∴四边形ABED是平行四边形,
∴AB=DE=CD,
∴△DCE是等腰三角形.
故选B.
点评:本题考查的是等腰梯形的性质及等腰三角形的判定定理,平行四边形的判定与性质,根据题意作出辅助线,构造出平行四边形及等腰三角形是解答此题的关键.
分析:过点D作DE∥AB,可得出四边形ABED是平行四边形,△DCE是等腰三角形,故可得出结论.
解答:
 解:过点D作DE∥AB,
解:过点D作DE∥AB,∵四边形ABCD是等腰梯形,
∴AD∥BC,
∴四边形ABED是平行四边形,
∴AB=DE=CD,
∴△DCE是等腰三角形.
故选B.
点评:本题考查的是等腰梯形的性质及等腰三角形的判定定理,平行四边形的判定与性质,根据题意作出辅助线,构造出平行四边形及等腰三角形是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
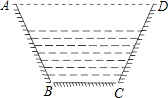 如图是一个等腰梯形状的水渠的横切面图,已知渠道底宽BC=2米,渠底与渠腰的夹角∠BCD=120°,渠腰CD=5米,求水渠的上口AD的长.
如图是一个等腰梯形状的水渠的横切面图,已知渠道底宽BC=2米,渠底与渠腰的夹角∠BCD=120°,渠腰CD=5米,求水渠的上口AD的长.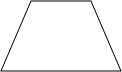 (2012•湖州一模)如图是一个等腰梯形,若在该梯形中添加一条线段,可把这个梯形分成一个平行四边形和一个三角形,则这个三角形一定是( )
(2012•湖州一模)如图是一个等腰梯形,若在该梯形中添加一条线段,可把这个梯形分成一个平行四边形和一个三角形,则这个三角形一定是( )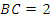 米,渠底与渠腰的夹角∠
米,渠底与渠腰的夹角∠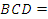 120°,渠腰
120°,渠腰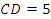 米,求水渠的上口AD的长.
米,求水渠的上口AD的长.