题目内容
【题目】如图,在平面直角坐标系中,△OAB的边OA在x轴的正半轴上,OA=AB,边OB的中点C在双曲线y=![]() 上,将△OAB沿OB翻折后,点A的对应点A′,正好落在双曲线y=
上,将△OAB沿OB翻折后,点A的对应点A′,正好落在双曲线y=![]() 上,△OAB的面积为6,则k为( )
上,△OAB的面积为6,则k为( )
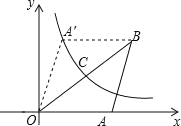
A.1 B.2 C.3 D.4
【答案】D
【解析】
试题分析:连接AA′,过点A′作A′E⊥x轴于点E,过点C作CF⊥x轴于点F,根据OA=AB结合翻折的特性可知∠A′BO=∠AOB,四边形OABA′为菱形,由中位线的性质结合平行线的性质可得出A′E=2CF,AE=2AF,再根据反比例函数系数k的几何意义和三角形面积公式即可得出OF=![]() OA,S△OCF=
OA,S△OCF=![]() ×
×![]() S△OAB=2,由此即可得出反比例系数k的值. 连接AA′,过点A′作A′E⊥x轴于点E,过点C作CF⊥x轴于点F,如图所示.
S△OAB=2,由此即可得出反比例系数k的值. 连接AA′,过点A′作A′E⊥x轴于点E,过点C作CF⊥x轴于点F,如图所示.
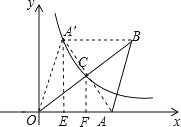
∵OA=AB, ∴∠AOB=∠ABO, 由翻折的性质可知:∠A′BO=∠ABO,A′B=AB,A′O=AO,
∴∠A′BO=∠AOB,四边形OABA′为菱形 ∴A′B∥OA.∵点C是线段OB的中点,A′E⊥x轴,CF⊥x轴,
∴A′E=2CF,AE=2AF, 又∵S△OA′E=S△OCF, ∴OF=2OE, ∴OE=EF=FA, ∴OF=![]() OA.
OA.
∵S△OAB=![]() OAA′E=6,S△OCF=
OAA′E=6,S△OCF=![]() OFCF, ∴S△OCF=
OFCF, ∴S△OCF=![]() ×
×![]() S△OAB=2. ∵S△OCF=
S△OAB=2. ∵S△OCF=![]() |k|=2,
|k|=2,
∴k=±4, ∵反比例函数在第一象限有图象, ∴k=4.

练习册系列答案
相关题目