Question

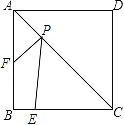
【题目】如图，正方形ABCD的边长为4，E为BC上的点，BE=1，F为AB的中点，P为AC上一个动点，则PF+PE的最小值为（ ）．

A.5B.C.D.无法确定

Answer 1

【答案】B

【解析】

如下图，作点E关于直线AC的对称点E′，连接E′F，则E′F的长即为所求的PE+PF的最小值，过F作FG⊥CD于G，在Rt△FGE′中由勾股定理求出FE′的长即可．

作点E关于直线AC的对称点E′，连接E′F，则E′F的长即为所求的PE+PF的最小值，

过F作FG⊥CD于G，则由题意可得CE′=CE，CG=BF，FG=BC，

∵BC=AB=4，BE=1，点F是AB的中点，

∴CE′=CE=BC-BE=3，CG=FB=2，FG=BC=4，

∴GE′=CE′-CG=3-2=1，

∴在Rt△E′FG中，E′F=．

故选：B．