题目内容
如图，一架2.5米长的梯子斜立在竖直的墙上，此时梯足B距底端O为0.7米，如果梯子顶端下滑0.4米，则梯子将滑出多少米？分析：在直角三角形ABC中，已知AB，BC根据勾股定理即可求AC的长度，根据AC=AA′+CA′即可求得CA′的长度，在直角三角形A′B′C中，已知AB=A′B′，CA′即可求得CB′的长度，根据BB′=CB′-CB即可求得BB′的长度．
解答：
解；在直角△ABC中，已知AB=2.5m，BC=0.7m，
则AC=
=2.4m，
∵AC=AA′+CA′
∴CA′=2m，
∵在直角△A′B′C中，AB=A′B′，且A′B′为斜边，
∴CB′=1.5m，
∴BB′=CB′-CB=1.5m-0.7m=0.8m
答：梯足向外移动了0.8m．
解；在直角△ABC中，已知AB=2.5m，BC=0.7m，则AC=
| 2．52-0．72 |
∵AC=AA′+CA′
∴CA′=2m，
∵在直角△A′B′C中，AB=A′B′，且A′B′为斜边，
∴CB′=1.5m，
∴BB′=CB′-CB=1.5m-0.7m=0.8m
答：梯足向外移动了0.8m．
点评：本题考查了勾股定理在实际生活中的应用，考查了勾股定理在直角三角形中的正确运用，本题中求CB′的长度是解题的关键．
练习册系列答案
相关题目
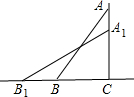如图，一架2.5米长的梯子AB，斜靠在一竖直的墙AC上，这时梯足B到墙底端C的距离为0.7米，如果梯子的顶端沿墙下滑0.4米，那么梯足将向外移多少米？
20、如图，一架2.5米长的梯子AB斜靠在竖直的墙AC上，这时梯子底部B到墙底端的距离为0.7米，考虑爬梯子的稳定性，现要将梯子顶部4沿墙下移0.4米到A′处，问梯子底部B将外移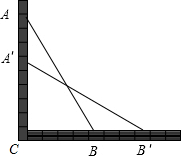
如图，一架2.5米长的梯子AB斜靠在竖直的墙AC上，这时梯子底部B到墙底端的距离为0.7米，考虑爬梯子的稳定性，现要将梯子顶部A沿墙下移0.4米到A′处，问梯子底部B将外移多少米？
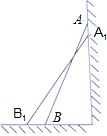子的顶端沿墙下滑0.4米，那么点B将向外移动多少米？