题目内容
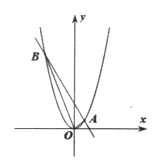
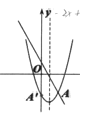
【题目】如图,已知直线y=-2x+1与抛物线y=x2-2x+c的一个交点为点A,作点A关于抛物线对称轴的对称点A,当A刚好落在y轴上时,c的值为____________.
【答案】-3
【解析】
由对称轴公式可得抛物线对称轴x=1，由A关于抛物线对称轴的对称点A'在y轴上，可推出A的横坐标为2，将x=2代入y=-2x+1，可求出A点坐标，再将A点坐标代入抛物线解析式即可求出c的值.
抛物线y=x2-2x+c的对称轴为
，
∵A关于抛物线对称轴的对称点A'在y轴上，
∴A的横坐标为2，
∵A点在直线上，
∴将x=2代入y=-2x+1得，y=-2×2+1=-3，
∴A点坐标为（2，-3）
∵A点在抛物线上，
∴将A（2，-3）代入y=x2-2x+c得，-3=22-2×2+c，
解得c=-3.
故答案为：-3.
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
