题目内容
给出下列命题:①对于实数u,v,定义一种运算“*“为:u*v=uv+v.若关于x的方程x*(a*x)=-
 没有实数根,则满足条件的实数a的取值范围是0<a<1;
没有实数根,则满足条件的实数a的取值范围是0<a<1;②设直线kx+(k+1)y-1=0(k为正整数)与坐标轴所构成的直角三角形的面积为Sk,则S1+S2+S3+…+S2008=
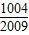 ;
;③函数y=-
 +
+ 的最大值为2;
的最大值为2;④甲、乙、丙3位同学选修课程,从4门课程中,甲选修2门,乙、丙各选修3门,则不同的选修方案共有48种.
其中真命题的个数有( )
A.1个
B.2个
C.3个
D.4个
【答案】分析:①根据新定义整理出一元二次方程,然后根据判别式△<0,方程没有实数根列式得到关于a的不等式,求解不等式即可判断;
②求出直线与坐标轴的交点坐标,再根据直角三角形的面积公式列式得到Sk的表达式,然后利用拆项法整理求解;
③先配方,再根据二次函数的最值问题求解;
④求出每一名同学的可能选修方法的种数,然后相乘即可得解.
解答:解:①根据新定义,x*(a*x)=x*(ax+x),
=x(ax+x)+(ax+x),
=(a+1)x2+(a+1)x,
所以,(a+1)x2+(a+1)x+ =0,
=0,
∵方程没有实数根,
∴△=(a+1)2-4(a+1)× <0,
<0,
即a(a+1)<0,
解得-1<a<0,故本小题错误;
②当y=0时,kx-1=0,解得x= ,
,
当x=0时,(k+1)y-1=0,解得y=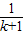 ,
,
所以,与x轴的交点坐标为(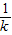 ,0),与y轴的交点坐标为(0,
,0),与y轴的交点坐标为(0,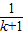 ),
),
∵k为正整数,
∴Sk= ×
×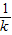 ×
×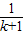 =
=
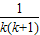 =
= (
(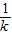 -
-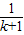 ),
),
∴S1+S2+S3+…+S2008= (1-
(1- +
+ -
- +
+ -
- +…+
+…+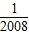 -
-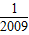 ),
),
= (1-
(1-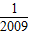 ),
),
= ×
×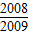 ,
,
=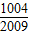 ,故本小题正确;
,故本小题正确;
③∵y=-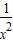 +
+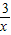 =-(
=-(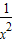 -
-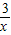 +
+ )+
)+ =-(
=-(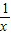 -
- )2+
)2+ ,
,
∴当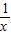 =
= ,即x=
,即x= 时,函数有最大值
时,函数有最大值 ,故本小题错误;
,故本小题错误;
④设4门课程分别为1,2,3,4,甲选修2门,可有1,2;1,3;1,4;2,3;2,4;3,4共6种情况,
同理乙,丙均可有1,2,3;1,2,4;2,3,4;1,3,4共4种情况,
所以,不同的选修方案共有6×4×4=96种,故本小题错误;
综上所述,真命题有②共1个.
故选A.
点评:本题考查了一元二次方程的根的判别式,一次函数图象上点的坐标特征,二次函数的最值问题,排列组合,综合性较强,难度较大,对同学们的能力要求比较高.
②求出直线与坐标轴的交点坐标,再根据直角三角形的面积公式列式得到Sk的表达式,然后利用拆项法整理求解;
③先配方,再根据二次函数的最值问题求解;
④求出每一名同学的可能选修方法的种数,然后相乘即可得解.
解答:解:①根据新定义,x*(a*x)=x*(ax+x),
=x(ax+x)+(ax+x),
=(a+1)x2+(a+1)x,
所以,(a+1)x2+(a+1)x+
 =0,
=0,∵方程没有实数根,
∴△=(a+1)2-4(a+1)×
 <0,
<0,即a(a+1)<0,
解得-1<a<0,故本小题错误;
②当y=0时,kx-1=0,解得x=
 ,
,当x=0时,(k+1)y-1=0,解得y=
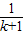 ,
,所以,与x轴的交点坐标为(
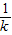 ,0),与y轴的交点坐标为(0,
,0),与y轴的交点坐标为(0,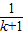 ),
),∵k为正整数,
∴Sk=
 ×
×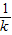 ×
×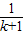 =
=
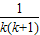 =
= (
(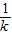 -
-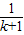 ),
),∴S1+S2+S3+…+S2008=
 (1-
(1- +
+ -
- +
+ -
- +…+
+…+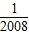 -
-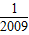 ),
),=
 (1-
(1-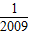 ),
),=
 ×
×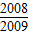 ,
,=
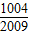 ,故本小题正确;
,故本小题正确;③∵y=-
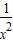 +
+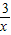 =-(
=-(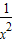 -
-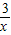 +
+ )+
)+ =-(
=-(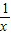 -
- )2+
)2+ ,
,∴当
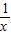 =
= ,即x=
,即x= 时,函数有最大值
时,函数有最大值 ,故本小题错误;
,故本小题错误;④设4门课程分别为1,2,3,4,甲选修2门,可有1,2;1,3;1,4;2,3;2,4;3,4共6种情况,
同理乙,丙均可有1,2,3;1,2,4;2,3,4;1,3,4共4种情况,
所以,不同的选修方案共有6×4×4=96种,故本小题错误;
综上所述,真命题有②共1个.
故选A.
点评:本题考查了一元二次方程的根的判别式,一次函数图象上点的坐标特征,二次函数的最值问题,排列组合,综合性较强,难度较大,对同学们的能力要求比较高.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 没有实数根,则满足条件的实数a的取值范围是0<a<1;
没有实数根,则满足条件的实数a的取值范围是0<a<1; ;
; +
+ 的最大值为2;
的最大值为2;