题目内容
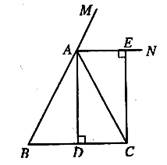
已知:如下图,在△ABC中,AB=AC,∠BAC=30°。点D为△ABC内一点,且DB=DC,∠DCB=30°。点E为BD延长线上一点,且AE=AB。
(1)求∠ADE的度数;
(2)若点M在DE上,且DM=DA,求证:ME=DC。
(1)求∠ADE的度数;
(2)若点M在DE上,且DM=DA,求证:ME=DC。

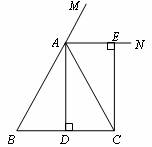
解:(1)如下图:

∵△ABC中,AB=AC,∠BAC=30°,
∴∠ABC=∠ACB= =75°
=75°
∵DB=DC,∠DCB=30°,
∴∠DBC=∠DCB=30°
∴∠1=∠ABC-∠DBC=75°-30°=45°
∵AB=AC,DB=DC,
∴AD所在直线垂直平分BC,
∴AD平分∠BAC,
∴∠2= ∠BAC=
∠BAC= =15°
=15°
∴∠ADE=∠1+∠2 =45°+15°=60°;
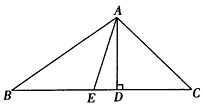
(2)连接AM,取BE的中点N,连接AN。如下图:

∵△ADM中,DM=DA,∠ADE=60°,
∴△ADM为等边三角形,
∵△ABE中,AB=AE,N为BE的中点,
∴BN=NE,且AN⊥BE,
∴DN=NM,
∴BN-DN =NE-NM,
即 BD=ME,
∵DB=DC,
∴ME = DC。

∵△ABC中,AB=AC,∠BAC=30°,
∴∠ABC=∠ACB=
 =75°
=75°∵DB=DC,∠DCB=30°,
∴∠DBC=∠DCB=30°
∴∠1=∠ABC-∠DBC=75°-30°=45°
∵AB=AC,DB=DC,
∴AD所在直线垂直平分BC,
∴AD平分∠BAC,
∴∠2=
 ∠BAC=
∠BAC= =15°
=15°∴∠ADE=∠1+∠2 =45°+15°=60°;
(2)连接AM,取BE的中点N,连接AN。如下图:

∵△ADM中,DM=DA,∠ADE=60°,
∴△ADM为等边三角形,
∵△ABE中,AB=AE,N为BE的中点,
∴BN=NE,且AN⊥BE,
∴DN=NM,
∴BN-DN =NE-NM,
即 BD=ME,
∵DB=DC,
∴ME = DC。

练习册系列答案
相关题目