题目内容
(满分l2分)如图,⊙O是Rt△ABC的外接圆,∠ABC=90°,点P是圆外一点,PA切⊙O于点A,且PA=PB.
(1)求证:PB是⊙O的切线;
(2)已知PA=
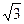 ,BC=1,求⊙O的半径.
,BC=1,求⊙O的半径.
(1)证明:连结OB.
∵OA=OB,∴∠OAB=∠OBA.
∵PA=PB,∴∠PAB=∠PBA.
∴∠OAB+∠PAB=∠OBA+∠PBA,
即∠PAO=∠PBO. ……2分
又∵PA是⊙O的切线,∴∠PAO=90°,
∴∠PBO=90°,∴OB⊥PB. ……4分
又∵OB是⊙O半径,∴PB是⊙O的切线. ……5分
(说明:还可连结OB,OP,利用△OAP≌OBP来证明OB⊥PB)
(2)解:连结OP,交AB于点D.
∵PA=PB,∴点P在线段AB的垂直平分线上.
∵OA=OB,∴点O在线段AB的垂直平分线上.
∴OP垂直平分线段AB. ……7分
∴∠PAO=∠PDA=90°.
又∵∠APO=∠DPA,∴△APO∽△DPA.
∴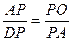 ,∴AP2=PO·DP.
,∴AP2=PO·DP.
又∵OD=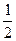 BC=
BC=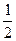 ,∴ PO(PO-OD)=AP2.
,∴ PO(PO-OD)=AP2.
即:PO 2一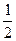 PO=(
PO=(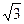 )2,解得PO=2. ……10分
)2,解得PO=2. ……10分
在Rt△APO中,OA=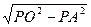 =1,即⊙O 的半径为l. ……12分
=1,即⊙O 的半径为l. ……12分
(说明:求半径时,还可证明△APA∽△ABC或在Rt△OAP中利用勾股定理)解析:
略
∵OA=OB,∴∠OAB=∠OBA.
∵PA=PB,∴∠PAB=∠PBA.
∴∠OAB+∠PAB=∠OBA+∠PBA,
即∠PAO=∠PBO. ……2分
又∵PA是⊙O的切线,∴∠PAO=90°,
∴∠PBO=90°,∴OB⊥PB. ……4分
又∵OB是⊙O半径,∴PB是⊙O的切线. ……5分
(说明:还可连结OB,OP,利用△OAP≌OBP来证明OB⊥PB)
(2)解:连结OP,交AB于点D.
∵PA=PB,∴点P在线段AB的垂直平分线上.
∵OA=OB,∴点O在线段AB的垂直平分线上.
∴OP垂直平分线段AB. ……7分
∴∠PAO=∠PDA=90°.
又∵∠APO=∠DPA,∴△APO∽△DPA.
∴
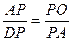 ,∴AP2=PO·DP.
,∴AP2=PO·DP. 又∵OD=
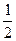 BC=
BC=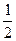 ,∴ PO(PO-OD)=AP2.
,∴ PO(PO-OD)=AP2.即:PO 2一
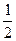 PO=(
PO=(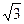 )2,解得PO=2. ……10分
)2,解得PO=2. ……10分在Rt△APO中,OA=
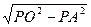 =1,即⊙O 的半径为l. ……12分
=1,即⊙O 的半径为l. ……12分(说明:求半径时,还可证明△APA∽△ABC或在Rt△OAP中利用勾股定理)解析:
略

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目

 ,且l1与x轴
,且l1与x轴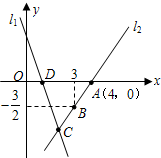
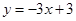 ,且l1与x轴
,且l1与x轴
 和
和 ,顶点O所经过的路程是这两段圆弧的长度之和,并且这两段圆弧
,顶点O所经过的路程是这两段圆弧的长度之和,并且这两段圆弧 ?
?
 和
和 ,顶点O所经过的路程是这两段圆弧的长度之和,并且这两段圆弧
,顶点O所经过的路程是这两段圆弧的长度之和,并且这两段圆弧 ?
?