Question

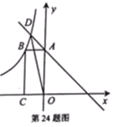
【题目】如图，在平面直角坐标系中，直线交轴于点，交反比例函数的图象于点，的图象过矩形的顶点，矩形的面积为4，连接.

(1)求反比例函数的表达式；

(2)求的面积.

Answer 1

【答案】（1）y=﹣；（2）．

【解析】

试题分析：（1）根据矩形的面积求出AB，求出反比例函数的解析式；

（2）解方程组求出反比例函数与一次函数的交点，确定点D的坐标，根据三角形的面积公式计算即可．

试题解析：（1）∵直线y=﹣x+3交y轴于点A，

∴点A的坐标为（0，3），即OA=3，

∵矩形OABC的面积为4，

∴AB=，

∵双曲线在第二象限，

∴k=4，

∴反比例函数的表达式为y=﹣；

（2）解方程组，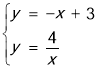

得 ，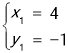

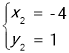
∵点D在第二象限，

∴点D的坐标为（﹣1，4），

∴△AOD的面积=×3×1=．