题目内容
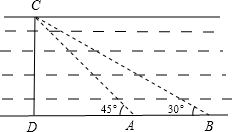
如图①,在平面直角坐标系中,O为坐标原点,边长为5的正三角形OAB的OA边在x轴的正半轴上.点C、D同时从点O出发,点C以1单位长/秒的速度向点A运动,点D为2个单位长/秒的速度沿折线OBA运动 .设运动时间为t秒,0<t<5.
.设运动时间为t秒,0<t<5.
(1)当0<t<
时,证明DC⊥OA;
(2)若△OCD的面积为S,求S与t的函数关系式;
(3)以点C为中心,将CD所在的直线顺时针旋转60°交AB边于点E,若以O、C、D、E为顶点的四边形是梯形,求点E的坐标.
 .设运动时间为t秒,0<t<5.
.设运动时间为t秒,0<t<5.(1)当0<t<
| 5 |
| 2 |
(2)若△OCD的面积为S,求S与t的函数关系式;
(3)以点C为中心,将CD所在的直线顺时针旋转60°交AB边于点E,若以O、C、D、E为顶点的四边形是梯形,求点E的坐标.
(1)作BG⊥OA于G.
在Rt△OBG中,
=cos∠BOA=cos60°=
,
而
=
,
∴
=
.
又∵∠DOC=∠BOG,
∴△DOC∽△BOG,
∴∠DCO=∠BGO=90°.
即DC⊥OA.
(2)当0<t<
时,
在Rt△OCD中,
CD=OD×sin60°=2t×
=
t.
∴S=
×OC×CD=
×t×
t=
t2;
当
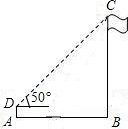
≤t<5时(如图2)
过点D作DH⊥OA于H.
在Rt△AHD中,
HD=AD×sin60°=(10-2t)×
=
(5-t).
S=
×OC×HD=
×t×
(5-t)=
t-
t2.
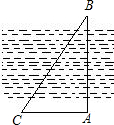
(3)当DE∥OC时,△DBE是等边三角形.(如图3)
BE=BD=5-2t.
在△CAE中,∠ECA=90°-∠DCE=30°,∠BAO=60°,
∴∠CEA=90°.
而AC=5-t,∴AE=
AC=
.
∴BE+AE=(5-2t)+
=5,
∴t=1.
因此AE=
=2.
过点E作EM⊥OA于M.
则EM=AE×sin60°=2×
=
,
AM=AE×cos60°=2×
=1,OM=OA-AM=4.
∴点E的坐标为(4,
).
当CD∥OE时(如图4),BD=2t-5.
∠OEA=90°,∴CD⊥AB.
而△OAB是等边三角形,
∴DE=BD-
AB=
.
∴2t-5=
.
∴t=
.
因此AE=
=
.
∴E的纵坐标为
×
=
,
横坐标为5-
×
=
,
∴点E的坐标为(
,
).
综上所述,点E的坐标为(4,
)或(
,
).
在Rt△OBG中,
| OG |
| OB |
| 1 |
| 2 |
而
| OC |
| OD |
| 1 |
| 2 |
∴
| OC |
| OD |
| OG |
| OB |
又∵∠DOC=∠BOG,
∴△DOC∽△BOG,
∴∠DCO=∠BGO=90°.
即DC⊥OA.
(2)当0<t<
| 5 |
| 2 |
在Rt△OCD中,
CD=OD×sin60°=2t×
| ||
| 2 |
| 3 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
当
| 5 |
| 2 |
过点D作DH⊥OA于H.

在Rt△AHD中,
HD=AD×sin60°=(10-2t)×
| ||
| 2 |
| 3 |
S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
5
| ||
| 2 |
| ||
| 2 |
(3)当DE∥OC时,△DBE是等边三角形.(如图3)
BE=BD=5-2t.
在△CAE中,∠ECA=90°-∠DCE=30°,∠BAO=60°,
∴∠CEA=90°.
而AC=5-t,∴AE=
| 1 |
| 2 |
| 5-t |
| 2 |
∴BE+AE=(5-2t)+
| 5-t |
| 2 |
∴t=1.
因此AE=
| 5-t |
| 2 |
过点E作EM⊥OA于M.
则EM=AE×sin60°=2×
| ||
| 2 |
| 3 |
AM=AE×cos60°=2×
| 1 |
| 2 |
∴点E的坐标为(4,
| 3 |
当CD∥OE时(如图4),BD=2t-5.
∠OEA=90°,∴CD⊥AB.
而△OAB是等边三角形,
∴DE=BD-
| 1 |
| 2 |
| 5 |
| 2 |
∴2t-5=
| 5 |
| 2 |
∴t=
| 15 |
| 4 |
因此AE=
| 5-t |
| 2 |
| 5 |
| 8 |
∴E的纵坐标为
| 5 |
| 8 |
| ||
| 2 |
| 5 |
| 16 |
| 3 |
横坐标为5-
| 5 |
| 8 |
| 1 |
| 2 |
| 75 |
| 16 |
∴点E的坐标为(
| 75 |
| 16 |
| 5 |
| 16 |
| 3 |
综上所述,点E的坐标为(4,
| 3 |
| 75 |
| 16 |
| 5 |
| 16 |
| 3 |

练习册系列答案
相关题目