Question

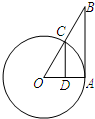（2012•和平区模拟）如图，AB与⊙O相切于点A，OB与⊙O交于点C，CD∥BA交OA于点D，⊙O的半径为1，则cos∠AOB的值等于（　　）

A．AB

B．OA

C．CD

D．OD

Answer 1

分析：由AB为圆O的切线，利用切线的性质得到OA与AB垂直，可得出∠OAB=90°，再由CD与AB平行，利用两直线平行同位角相等得到∠ODC=90°，在直角三角形OCD中，利用锐角三角函数定义及OC=1，即可表示出cos∠AOB．

解答：解：∵AB与圆O相切，
∴OA⊥AB，
∴∠OAB=90°，
又∵CD∥AB，
∴∠ODC=∠OAB=90°，
在Rt△OCD中，OC=1，
则cos∠AOB=

OD

OC

=OD．
故选D．

点评：此题考查了切线的性质，平行线的性质，以及锐角三角函数定义，熟练掌握性质是解本题的关键．