题目内容
【题目】(本题10分) 如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.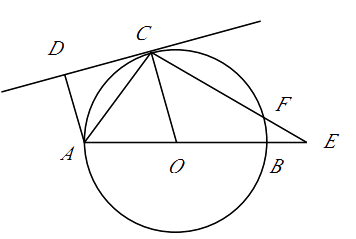
(1)求证:AC平分∠DAO.
(2)若∠DAO=105°,∠E=30°.
①求∠OCE的度数.
②若⊙O的半径为2 ![]() ,求线段EF的长.
,求线段EF的长.
【答案】
(1)
解:∵直线与⊙O相切,
∴OC⊥CD;
又∵AD⊥CD,
∴AD//OC,
∴∠DAC=∠OCA;
又∵OC=OA,
∴∠OAC=∠OCA,
∴∠DAC=∠OAC;
∴AC平分∠DAO.
(2)
解:①∵AD//OC,∠DAO=105°,
∴∠EOC=∠DAO=105°;
∵∠E=30°,
∴∠OCE=45°.
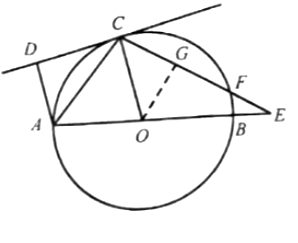
②作OG⊥CE于点G,可得FG=CG,
∵OC=2![]() ,∠OCE=45°.
,∠OCE=45°.
∴CG=OG=2,
∴FG=2;
∵在RT△OGE中,∠E=30°,
∴GE=2![]() ,
,
∴EF=GE-FG=2![]() -2.
-2.
【解析】(1)利用了切线的性质,平行线的判定和性质,等边对等角,角平分线的判定即可得证。
(2)①根据(1)得出的AD//OC,从而得出同位角相等,再利用三角形的内角和定理即可求出答案;②作OG⊥CE于点G,可得FG=CG,根据等边对等角得出CG=OG=FG=2,在根据勾股定理得出GE,从而求出EF=GE-FG.
【考点精析】认真审题,首先需要了解平行线的判定与性质(由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质),还要掌握三角形的内角和外角(三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角)的相关知识才是答题的关键.

 阅读快车系列答案
阅读快车系列答案