题目内容
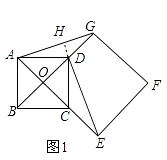
【题目】如图1,点O是正方形ABCD两对角线的交点,分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG、DE. n
n
(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转角(0°< ![]() <360°)得到正方形OE’F’G’,如图2.
<360°)得到正方形OE’F’G’,如图2.
①在旋转过程中,当∠OAG’是直角时,求 ![]() 的度数;
的度数;
②若正方形ABCD的边长为1,在旋转过程中,求AF’长的最大值和此时 ![]() 的度数,直接写出结果不必说明理由.
的度数,直接写出结果不必说明理由.
【答案】
(1)证明:如图1,延长ED交AG于点H,
∵点O是正方形ABCD两对角线的交点,
∴OA=OD,OA⊥OD,
∵OG=OE,
在△AOG和△DOE中,
 ,
,
∴△AOG≌△DOE,
∴∠AGO=∠DEO,
∵∠AGO+∠GAO=90°,
∴∠GAO+∠DEO=90°,
∴∠AHE=90°,
即DE⊥AG;
(2)解:①在旋转过程中,∠OAG′成为直角有两种情况:
(Ⅰ)α由0°增大到90°过程中,当∠OAG′=90°时,
∵OA=OD= ![]() OG=
OG= ![]() OG′,
OG′,
∴在Rt△OAG′中,sin∠AG′O= ![]() =
= ![]() ,
,
∴∠AG′O=30°,
∵OA⊥OD,OA⊥AG′,
∴OD∥AG′,
∴∠DOG′=∠AG′O=30°,
即α=30°;
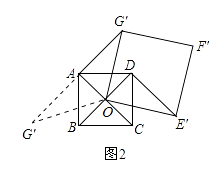
(Ⅱ)α由90°增大到180°过程中,当∠OAG′=90°时,
同理可求∠BOG′=30°,
∴α=180°30°=150°.
综上所述,当∠OAG′=90°时,α=30°或150°.
②如图3,当旋转到A. O、F′在一条直线上时,AF′的长最大,
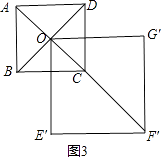
∵正方形ABCD的边长为1,
∴OA=OD=OC=OB= ![]() ,
,
∵OG=2OD,
∴OG′=OG= ![]() ,
,
∴OF′=2,
∴AF′=AO+OF′= ![]() +2,
+2,
∵∠COE′=45°,
∴此时α=315°
【解析】(1)延长ED交AG于点H,根据正方形的性质得出得出OA=OD,OG=OE,再证△AOG≌△DOE,得出∠AGO=∠DEO,根据等量代换证明结论。
(2)①根据题意和锐角正弦的概念以及特殊角的三角函数值得到∠AG′O=30°,分两种情况求出α的度数。
②根据正方形的性质分别求出OA和OF的长,根据旋转变换的性质求出AF′长的最大值和此时α的度数。

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案




