Question

【题目】如图，“和谐号”高铁列车的小桌板收起时近似看作与地面垂直，小桌板的支架底端与桌面顶端的距离OA=75厘米．展开小桌板使桌面保持水平，此时CB⊥AO，∠AOB=∠ACB=37°，且支架长OB与BC的长度之和等于OA的长度．

（1）求∠CBO的度数；

（2）求小桌板桌面的宽度BC．（参考数据sin37°≈0.6，cos37°≈0.8，tan37°≈0.75）

Answer 1

【答案】（1）127°；（2）37.5厘米．

【解析】

试题分析：（1）如图延长CB交OA于E，∠CBO是三角形OEB的外角，根据三角形的外角性质可得：∠OBC=∠AOB+∠BEO即可计算；（2）延长OB交AC于F．设BC=x，根据OB与BC的长度之和等于OA的长度．则OB=OA﹣BC=75﹣x，在Rt△BCF中利用37度的正弦函数求出BF，再在Rt△AOF中根据cos37°=，列出方程即可求出BC．

试题解析：（1）如图，延长CB交OA于E，

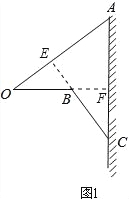
∵OA⊥BC，∴∠BEO=90°，∵∠AOB=37°，∴∠OBC=∠AOB+∠BEO=37°+90°=127°；（2）如上图，延长OB交AC于F．设BC=x，根据OB与BC的长度之和等于OA的长度，则OB=OA﹣BC=75﹣x，∵∠AOB=∠ACB，∠OBE=∠CBF，∠AOB+∠OBE=90°，∴∠ACB+∠CBF=90°，∴∠BFC=90°，在Rt△BFC中，∵sin37°=，∴BF=0.6x，OF=75﹣0.4x，在Rt△OAF中，cos37°=，∴=0.8，∴x=37.5厘米．∴小桌板桌面的宽度BC的长度为37.5厘米．