题目内容
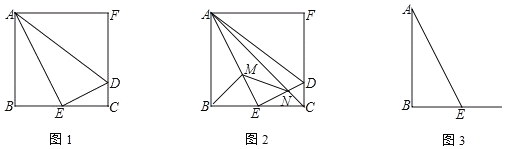
【题目】已知:正方形ABCF中,E为BC中点,点D在CF上,AB=4,CD=1.
(1)判断△AED的形状,并证明;
(2)AC交DE于点N,M在AE上,且满足BM2﹣ME2=EN2﹣CN2,求证:BM⊥AC;
(3)若△APE是以AE为斜边的等腰直角三角形,直接写出BP的长.
【答案】(1)△AED是直角三角形,证明见解析;(2)证明见解析;(3)BP=![]() 或
或![]() .
.
【解析】
(1)根据△AED是直角三角形,并通过AE2+DE2=AD2来进行判断;
(2)由题意延长BM交AC于H,延长NE到G,使EG=EN,连接BG、MG,并通过构造ME是线段GN的垂直平分线,可得MG=MN,进而通过BM2﹣ME2=EN2﹣CN2可得BM2+CN2=MG2,从而得到∠MBG=90°;由构造所得△BEG≌△CEN,从而证明BG∥AC,所以∠AHB=90°,从而证明BM⊥AC;
(3)根据题意,运用矩形和正方形性质以及分类讨论的思维分两种情形分别进行分析求解即可.
解:(1)△AED是直角三角形.
证明:∵正方形ABCF,AB=4,
∴BC=CF=AF=AB=4,∠B=∠C=∠F=90°,
∵CD=1,
∴DF=CF﹣CD=3,
∵E为BC中点,
∴BE=CE=2,
在Rt△ABE中,∠B=90°,由勾股定理得AE2=AB2+BE2=20
在Rt△CDE中,∠C=90°,由勾股定理得DE2=CE2+CD2=5
在Rt△AFD中,∠F=90°,由勾股定理得AD2=AF2+DF2=25
∵AE2+DE2=20+5=25=AD2,
∴△AED是直角三角形.
(2)如图,延长BM交AC于H,延长NE到G,使EG=EN,连接BG、MG
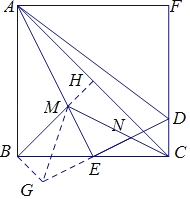
由(1)知,∠AED=90°,
∴ME⊥GN,
又∵EG=EN,
∴MG=MN,
∵BM2﹣ME2=EN2﹣CN2,
∴BM2+CN2=EN2+ME2=MN2,
∴BM2+CN2=MG2,
∴△BMG是直角三角形,且∠MBG=90°,
∵E为BC中点,
∴BE=CE,
在△BEG和△CEN中
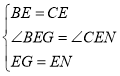 ,
,
∴△BEG≌△CEN(SAS),
∴∠GBE=∠NCE,
∴BG∥AC,
∴∠AHB=∠MBG=90°,
∴BM⊥AC.
(3)BP=3![]() 或
或![]() .
.
解析如下:
如图,以AE为斜边作等腰直角三角形APE,连接BP.作PM⊥AB于M,作PN⊥BE于N,
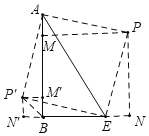
∴∠AMP=∠PNE=90°,PA=PE,
∵∠ABE=∠APE=90°,
∴∠BAP+∠BEP=180°,
∵∠BEP+∠PEN=180°,
∴∠BAP=∠PEN,
在△AMP和△ENP中
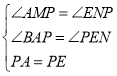 ,
,
∴△AMP≌△ENP(AAS),
∴AM=EN,PM=PN,
∵∠ABE=∠PMB=∠PNE=90°,
∴四边形PMBN是矩形,
又∵PM=PN,
∴四边形PMBN是正方形,
∴BM=BN,
∵BM+BN=AB﹣AM+BE+EN=AB+BE=6,
∴BM=BN=3,
∵BP是正方形PMBN的对角线,
∴BP![]() BM=3
BM=3![]() ,
,
当点P在直线AE的下方时,同法可得BP'![]() BM'
BM'![]() ,
,
综上所述满足条件的BP的长为3![]() 或
或![]() .
.