题目内容
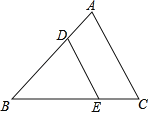
【题目】如图，已知点D，E分别为AB，BC上的点，连接DE，∠A＝70°，∠ADE＝110°．
（1）求证：∠C＝∠BED；
（2）作图：过D点作DF⊥BC，垂足为F，连接AE，若∠EDF＝∠EAC＝28°，求∠C的度数．
【答案】（1）详见解析；（2）62°．
【解析】
（1）根据∠A＝70°，∠ADE＝110°．可得∠A+∠ADE＝180°．得DE∥AC，即可证明∠C＝∠BED；
（2）过D点作DF⊥BC，垂足为F，连接AE，DE∥AC，∠EDF＝∠EAC＝28°，可得∠EAC＝∠AED＝EDF＝28°，得DF∥AE，可得∠AEB＝∠DFB＝90°，根据直角三角形两个锐角互余即可得∠C的度数．
解：（1）证明：∵∠A＝70°，∠ADE＝110°．
∴∠A+∠ADE＝180°．
∴DE∥AC，
∴∠C＝∠BED；
（2）如图所示，
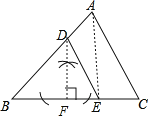
过D点作DF⊥BC，垂足为F，连接AE，
∵DE∥AC，∠EDF＝∠EAC＝28°
∴∠EAC＝∠AED＝EDF＝28°，
∴DF∥AE，
∵DF⊥BC，
∴∠AEB＝∠DFB＝90°，
∵∠C＝∠BED，
∴∠C＝∠BED＝90°﹣28°＝62°．
练习册系列答案
相关题目
【题目】我市一水果销售公司，需将一批鲜桃运往某地，有汽车、火车、运输工具可供选择，两种运输工具的主要参考数据如下：
运输工具 | 途中平均速度（单位：千米/时） | 途中平均费用（单位：元/千米） | 装卸时间（单位：小时） | 装卸费用（单位：元） |
汽车 | 75 | 8 | 2 | 1000 |
火车 | 100 | 6 | 4 | 2000 |
若这批水果在运输过程中（含装卸时间）的损耗为150元/时，设运输路程为x（
）千米，用汽车运输所需总费用为y1元，用火车运输所需总费用为y2元.
（1）分别求出y1、y2与x的关系式；
（2）那么你认为采用哪种运输工具比较好？
