题目内容
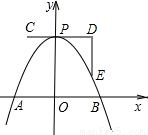
 如图,一条抛物线与x轴交于A、B两点,且顶点P在折线C-D-E上移动,若点C、D、E的坐标分别为(-1,-4),(2,-4),(3,-1),点A的横坐标的最小值为-3,则点B的横坐标的最大值为
如图,一条抛物线与x轴交于A、B两点,且顶点P在折线C-D-E上移动,若点C、D、E的坐标分别为(-1,-4),(2,-4),(3,-1),点A的横坐标的最小值为-3,则点B的横坐标的最大值为
- A.1
- B.2
- C.3
- D.4
D
分析:抛物线在平移过程中形状没有发生变化,因此函数解析式的二次项系数在平移前后不会改变.首先,当点A横坐标取最小值时,函数的顶点在C点,根据待定系数法可确定抛物线的解析式;而点B横坐标取最大值时,抛物线的顶点应移动到E点,结合前面求出的二次项系数以及E点坐标可确定此时抛物线的解析式,进一步能求出此时点B的坐标,即点B的横坐标最大值.
解答:由图知:当点A的横坐标为-3时,抛物线顶点取(-1,-4),设该抛物线的解析式为:y=a(x+1)2-4,代入点A坐标,得:
0=a(-3+1)2-4,a=1,
即:点A的横坐标的最小值-3时,抛物线的解析式为:y=(x+1)2-4.
当B点横坐标取最大值时,抛物线顶点应取(3,-1),则此时抛物线的解析式:y=(x-3)2-1=x2-6x+8=-(x-2)(x-4),即与x轴的交点为(2,0)或(4,0),
∴点B的横坐标的最大值为4.
故选D.
点评:此题主要考查了二次函数综合题,解答该题的关键在于读透题意,要注意的是抛物线在平移过程中形状并没有发生变化,改变的是顶点坐标.注意抛物线顶点所处的C、E两个关键位置,前者能确定函数解析式、后者能得到要求的结果.
分析:抛物线在平移过程中形状没有发生变化,因此函数解析式的二次项系数在平移前后不会改变.首先,当点A横坐标取最小值时,函数的顶点在C点,根据待定系数法可确定抛物线的解析式;而点B横坐标取最大值时,抛物线的顶点应移动到E点,结合前面求出的二次项系数以及E点坐标可确定此时抛物线的解析式,进一步能求出此时点B的坐标,即点B的横坐标最大值.
解答:由图知:当点A的横坐标为-3时,抛物线顶点取(-1,-4),设该抛物线的解析式为:y=a(x+1)2-4,代入点A坐标,得:
0=a(-3+1)2-4,a=1,
即:点A的横坐标的最小值-3时,抛物线的解析式为:y=(x+1)2-4.
当B点横坐标取最大值时,抛物线顶点应取(3,-1),则此时抛物线的解析式:y=(x-3)2-1=x2-6x+8=-(x-2)(x-4),即与x轴的交点为(2,0)或(4,0),
∴点B的横坐标的最大值为4.
故选D.
点评:此题主要考查了二次函数综合题,解答该题的关键在于读透题意,要注意的是抛物线在平移过程中形状并没有发生变化,改变的是顶点坐标.注意抛物线顶点所处的C、E两个关键位置,前者能确定函数解析式、后者能得到要求的结果.

练习册系列答案
相关题目
 (2012•大连)如图,一条抛物线与x轴相交于A、B两点,其顶点P在折线C-D-E上移动,若点C、D、E的坐标分别为(-1,4)、(3,4)、(3,1),点B的横坐标的最小值为1,则点A的横坐标的最大值为( )
(2012•大连)如图,一条抛物线与x轴相交于A、B两点,其顶点P在折线C-D-E上移动,若点C、D、E的坐标分别为(-1,4)、(3,4)、(3,1),点B的横坐标的最小值为1,则点A的横坐标的最大值为( )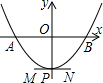 (2013•大连一模)如图,一条抛物线与x轴相交于A、B两点(点A在点B的左侧),其顶点P在线段MN上移动.若点M、N的坐标分别为(-1,-2)、(1,-2),点B的横坐标的最大值为3,则点A的横坐标的最小值为( )
(2013•大连一模)如图,一条抛物线与x轴相交于A、B两点(点A在点B的左侧),其顶点P在线段MN上移动.若点M、N的坐标分别为(-1,-2)、(1,-2),点B的横坐标的最大值为3,则点A的横坐标的最小值为( )