题目内容
如图,已知点A为双曲线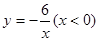 上的一点,AB⊥x轴,OA=4,且OA的垂直平分线交x轴于点C,连接AC,则△ABC的周长为 。
上的一点,AB⊥x轴,OA=4,且OA的垂直平分线交x轴于点C,连接AC,则△ABC的周长为 。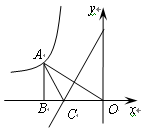
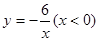 上的一点,AB⊥x轴,OA=4,且OA的垂直平分线交x轴于点C,连接AC,则△ABC的周长为 。
上的一点,AB⊥x轴,OA=4,且OA的垂直平分线交x轴于点C,连接AC,则△ABC的周长为 。
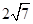
由双曲线解析式可知,OB×AB=6,由勾股定理可知OB2+AB2=OA2=42,由此可求OB+AB,由垂直平分线的性质可知AC=CO,则AB+BC+AC=AB+BC+CO=AB+BO.
解:∵点A在双曲线y=-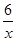 上,
上,
∴OB×AB=6,
又在Rt△ABO中,OB2+AB2=OA2=42,
∴(OB+AB)2=OB2+AB2+2OB×AB=16+12=28,
∴OB+AB=2 ,
,
∵OA的垂直平分线交x轴于点C,
∴AC=CO,
∴AB+BC+AC=AB+BC+CO=AB+BO=2 .
.
故答案为:2 .
.
本题考查了反比例函数的综合运用.关键是双曲线解析式与相关线段的关系,勾股定理,通过代数式的变形求AB+BO的值.
解:∵点A在双曲线y=-
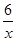 上,
上,∴OB×AB=6,
又在Rt△ABO中,OB2+AB2=OA2=42,
∴(OB+AB)2=OB2+AB2+2OB×AB=16+12=28,
∴OB+AB=2
 ,
,∵OA的垂直平分线交x轴于点C,
∴AC=CO,
∴AB+BC+AC=AB+BC+CO=AB+BO=2
 .
.故答案为:2
 .
.本题考查了反比例函数的综合运用.关键是双曲线解析式与相关线段的关系,勾股定理,通过代数式的变形求AB+BO的值.

练习册系列答案
相关题目
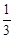 x2 和反比例函数y2的图象有一个交点是 A(
x2 和反比例函数y2的图象有一个交点是 A(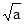 ,-1).
,-1).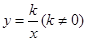 的图象上,过点P作PM⊥x轴于点
的图象上,过点P作PM⊥x轴于点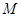 ,PN⊥y轴于点N,若矩形PMON的面积为6,则
,PN⊥y轴于点N,若矩形PMON的面积为6,则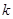 的值是
的值是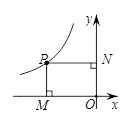
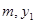 )和(
)和( )是反比例函数
)是反比例函数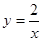 图像上的两点,当m满足
图像上的两点,当m满足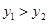 。
。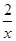 上的任意一点,PD⊥x轴于点D,则△POD的面积是__________.
上的任意一点,PD⊥x轴于点D,则△POD的面积是__________.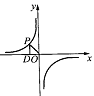
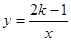 的图象经过第二、四象限,则k的取值范围是 ▲
的图象经过第二、四象限,则k的取值范围是 ▲  交于A、B两点,过点A作
交于A、B两点,过点A作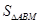 =2,则k的值是 ( )
=2,则k的值是 ( )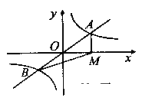
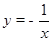 的图象经过点
的图象经过点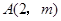 ,则
,则 的值是 ( )
的值是 ( )