题目内容
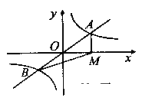
如图,直线y=mx与双曲线y= 交于A、B两点,过点A作
交于A、B两点,过点A作
AM⊥x轴,垂足为M,连结BM,若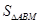 =2,则k的值是 ( )
=2,则k的值是 ( )
A.2 B、m-2 C、m D、4
 交于A、B两点,过点A作
交于A、B两点,过点A作AM⊥x轴,垂足为M,连结BM,若
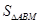 =2,则k的值是 ( )
=2,则k的值是 ( )
A.2 B、m-2 C、m D、4
A
由题意得:S△ABM=2S△AOM,又S△AOM= 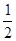 |k|,则k的值即可求出.
|k|,则k的值即可求出.
解:设A(x,y),
∵直线y=mx与双曲线y= 交于A、B两点,
交于A、B两点,
∴B(-x,-y),
∴S△BOM=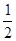 |xy|,S△AOM=
|xy|,S△AOM=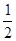 |xy|,
|xy|,
∴S△BOM=S△AOM,
∴S△ABM=S△AOM+S△BOM=2S△AOM=2,S△AOM=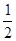 |k|=1,则k=±2.
|k|=1,则k=±2.
又由于反比例函数位于一三象限,k>0,故k=2.
故选A.
本题主要考查了反比例函数y= 中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点.
中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点.
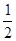 |k|,则k的值即可求出.
|k|,则k的值即可求出.解:设A(x,y),
∵直线y=mx与双曲线y=
 交于A、B两点,
交于A、B两点,∴B(-x,-y),
∴S△BOM=
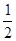 |xy|,S△AOM=
|xy|,S△AOM=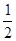 |xy|,
|xy|,∴S△BOM=S△AOM,
∴S△ABM=S△AOM+S△BOM=2S△AOM=2,S△AOM=
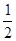 |k|=1,则k=±2.
|k|=1,则k=±2.又由于反比例函数位于一三象限,k>0,故k=2.
故选A.
本题主要考查了反比例函数y=
 中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点.
中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
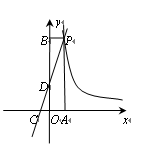
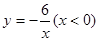 上的一点,AB⊥x轴,OA=4,且OA的垂直平分线交x轴于点C,连接AC,则△ABC的周长为 。
上的一点,AB⊥x轴,OA=4,且OA的垂直平分线交x轴于点C,连接AC,则△ABC的周长为 。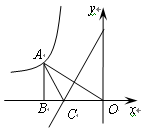
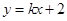 的图象与反比例函数
的图象与反比例函数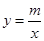 的
的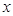 轴、
轴、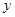 轴于点C、D,
轴于点C、D,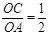 .
.
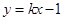 的图象与反比例函数
的图象与反比例函数 的图象交于A、B两点,其中A点坐标为(2,1).
的图象交于A、B两点,其中A点坐标为(2,1).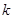 、
、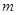 的值;
的值;
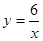 的图像上的一点,PQ垂直于x轴,垂足为Q,那么△POQ的面积为( )
的图像上的一点,PQ垂直于x轴,垂足为Q,那么△POQ的面积为( )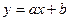 的图象与反比例函数
的图象与反比例函数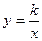 的图象交于
的图象交于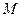 、
、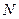 两点.
两点.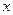 的取值范围.
的取值范围.
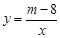 (m为常数)的图象经过点A(-1,6),则m的值为 .
(m为常数)的图象经过点A(-1,6),则m的值为 . 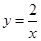 ,下列说法不正确的是( )
,下列说法不正确的是( )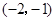 在它的图象上
在它的图象上 时,
时,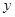 随
随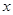 的增大而增大
的增大而增大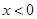 时,
时,