题目内容
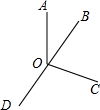如图所示，从点O依次引四条射线，OA、OB、OC、OD，如果∠AOB、∠BOC、∠COD、∠DOA的度之比为1：2：3：4，求∠BOC的度数．
解：设∠AOB=x，根据题意得：∠BOC=2x，∠COD=3x，∠DOA=4x，
∴x+2x+3x+4x=360゜，
解得：x=36゜，
∴∠BOC=72゜．
分析：设∠AOB=x，则∠BOC=2x，∠COD=3x，∠DOA=4x，利用周角定义列出方程，求出方程的解得到x的值，即可确定出∠BOC的度数．
点评：此题考查了角的计算，利用了方程的思想，是一道基本题型．
∴x+2x+3x+4x=360゜，
解得：x=36゜，
∴∠BOC=72゜．
分析：设∠AOB=x，则∠BOC=2x，∠COD=3x，∠DOA=4x，利用周角定义列出方程，求出方程的解得到x的值，即可确定出∠BOC的度数．
点评：此题考查了角的计算，利用了方程的思想，是一道基本题型．
练习册系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
相关题目
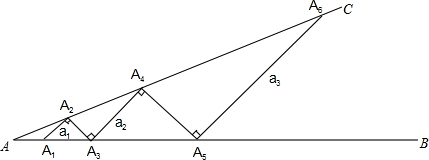
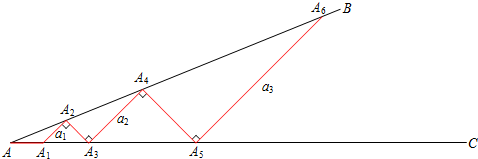
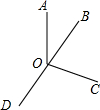如图所示，从点O依次引四条射线，OA、OB、OC、OD，如果∠AOB、∠BOC、∠COD、∠DOA的度之比为1：2：3：4，求∠BOC的度数．