题目内容
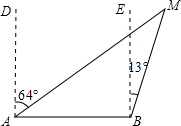 如图,一艘轮船在A处看见巡逻艇M在其北偏东64°的方向上,此时一艘客船在B处看见巡逻艇M在其北偏东13°的方向上,则此时从巡逻艇上看这两艘船的视角∠AMB=
如图,一艘轮船在A处看见巡逻艇M在其北偏东64°的方向上,此时一艘客船在B处看见巡逻艇M在其北偏东13°的方向上,则此时从巡逻艇上看这两艘船的视角∠AMB=51°
51°
.分析:根据AD∥BE,得出∠DAB+∠EBA=180°,再根据∠DAM=64°,求出∠ABE+∠EAB=180°-64°=116°,最后根据∠EBM=13°,求出∠EAB+∠ABM=∠EAB+∠EBA+∠EBM=116°+13°=129°,最后根据三角形的内角和定理得出∠AMB的度数.
解答:解:∵AD∥BE,
∴∠DAB+∠EBA=180°,
∵∠DAM=64°,
∴∠ABE+∠EAB=180°-64°=116°,
∵∠EBM=13°,
∴∠EAB+∠ABM=∠EAB+∠EBA+∠EBM=116°+13°=129°,
∴∠AMB=180°-129°=51°.
故答案为:51°.
∴∠DAB+∠EBA=180°,
∵∠DAM=64°,
∴∠ABE+∠EAB=180°-64°=116°,
∵∠EBM=13°,
∴∠EAB+∠ABM=∠EAB+∠EBA+∠EBM=116°+13°=129°,
∴∠AMB=180°-129°=51°.
故答案为:51°.
点评:此题考查了方向角,用到的知识点是平行线的性质、三角形的内角和定理、方向角,关键是根据有关性质求出角的度数.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 50、如图,一艘轮船在A处看见巡逻艇M在其北偏东62°的方向上,此时一艘客船在B处看见巡逻艇M在其北偏东13°的方向上,试求此时从巡逻艇上看这两艘船的视角∠AMB的度数.
50、如图,一艘轮船在A处看见巡逻艇M在其北偏东62°的方向上,此时一艘客船在B处看见巡逻艇M在其北偏东13°的方向上,试求此时从巡逻艇上看这两艘船的视角∠AMB的度数.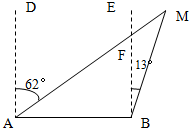 11、如图,一艘轮船在A处看见巡逻艇M在其北偏东62°的方向上,此时一艘客船在B处看见巡逻艇M在其北偏东13°的方向上,则此时从巡逻艇上看这两艘船的视角∠AMB=
11、如图,一艘轮船在A处看见巡逻艇M在其北偏东62°的方向上,此时一艘客船在B处看见巡逻艇M在其北偏东13°的方向上,则此时从巡逻艇上看这两艘船的视角∠AMB=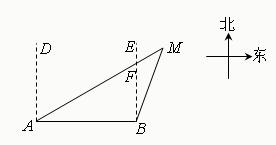 18、如图,一艘轮船在A处看见巡逻艇M在其北偏东60°的方向上,同时一艘客船在B处看见巡逻艇M在其北偏东20°的方向上,试求此时从巡逻艇上看这两艘船的视角∠AMB的度数.
18、如图,一艘轮船在A处看见巡逻艇M在其北偏东60°的方向上,同时一艘客船在B处看见巡逻艇M在其北偏东20°的方向上,试求此时从巡逻艇上看这两艘船的视角∠AMB的度数.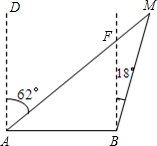 如图,一艘轮船在A处看见巡逻艇M在其北偏东62°的方向上,此时一艘客船在B处看见巡逻艇M在其北偏东18°的方向上,则此时从巡逻艇上看这两艘船的视角∠AMB=
如图,一艘轮船在A处看见巡逻艇M在其北偏东62°的方向上,此时一艘客船在B处看见巡逻艇M在其北偏东18°的方向上,则此时从巡逻艇上看这两艘船的视角∠AMB=