题目内容
【题目】如图,直线y=kx+b(k、b为常数)分别与x轴、y轴交于点A(﹣4,0)、B(0,3),抛物线y=﹣x2+2x+1与y轴交于点C,点E在抛物线y=﹣x2+2x+1的对称轴上移动,点F在直线AB上移动,CE+EF的最小值是( )
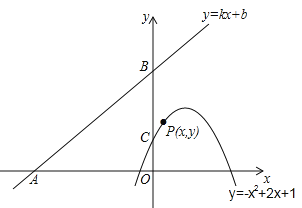
A. 1.4 B. 2.5 C. 2.8 D. 3
【答案】C
【解析】分析:由A、B两点的坐标,利用待定系数法可求得直线解析式;过P作PH⊥AB于点H,过H作HQ⊥x轴,过P作PQ⊥y轴,两垂线交于点Q,则可证明△PHQ∽△BAO,设H(m, ![]() m+3),利用相似三角形的性质可得到d与x的函数关系式,设C点关于抛物线对称轴的对称点为C′,由对称的性质可得CE=C′E,则可知当F、E、C′三点一线且C′F与AB垂直时CE+EF最小,由C点坐标可确定出C′点的坐标,利用所求函数关系式可求得d的值,即可求得CE+EF的最小值.
m+3),利用相似三角形的性质可得到d与x的函数关系式,设C点关于抛物线对称轴的对称点为C′,由对称的性质可得CE=C′E,则可知当F、E、C′三点一线且C′F与AB垂直时CE+EF最小,由C点坐标可确定出C′点的坐标,利用所求函数关系式可求得d的值,即可求得CE+EF的最小值.
详解: (1)由题意可得
![]() ,解得
,解得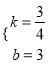 ,
,
∴直线解析式为y=![]() x+3;
x+3;
过P作PH⊥AB于点H,过H作HQ⊥x轴,过P作PQ⊥y轴,两垂线交于点Q,
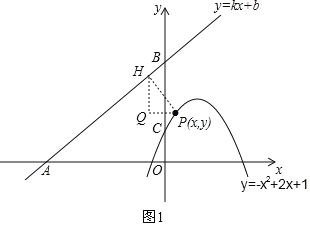
则∠AHQ=∠ABO,且∠AHP=90°,
∴∠PHQ+∠AHQ=∠BAO+∠ABO=90°,
∴∠PHQ=∠BAO,且∠AOB=∠PQH=90°,
∴△PQH∽△BOA,
∴![]() ,
,
设H(m, ![]() m+3),则PQ=xm,HQ=
m+3),则PQ=xm,HQ=![]() m+3(x+2x+1),
m+3(x+2x+1),
∵A(4,0),B(0,3),
∴OA=4,OB=3,AB=5,且PH=d,
∴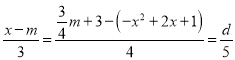
整理消去m可得d=![]() ,
,
∴d与x的函数关系式为d=![]() ,
,
设C点关于抛物线对称轴的对称点为C′,由对称的性质可得CE=C′E,
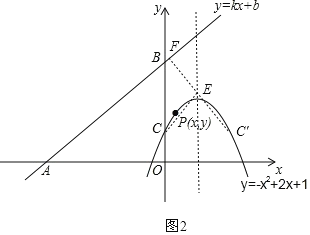
∴CE+EF=C′E+EF,
∴当F. E.C′三点一线且C′F与AB垂直时CE+EF最小,
∵C(0,1),
∴C′(2,1),
由(2)可知当x=2时,d=![]() =2.8,
=2.8,
即CE+EF的最小值为2.8.
点睛:
本题为二次函数的综合应用,涉及待定系数法、相似三角形的判定和性质、二次函数的性质、轴对称的性质等知识.注意待定系数法的应用,构造相似三角形是解题的重要步骤,确定出E点的位置是解题的关键.本题考查知点较多,综合性较强,难度适中.

【题目】某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作.已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果每千克的利润为3元,那么每天可售出250千克.
小红:如果以13元/千克的价格销售,那么每天可获取利润750元.
【利润=(销售价-进价)![]() 销售量】
销售量】
(1)请根据他们的对话填写下表:
销售单价x(元/kg) | 10 | 11 | 13 |
销售量y(kg) |
(2)请你根据表格中的信息判断每天的销售量y(千克)与销售单价x(元)之间存在怎样的函数关系.并求y(千克)与x(元)(x>0)的函数关系式;
(3)设该超市销售这种水果每天获取的利润为W元,求W与x的函数关系式.当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?