题目内容
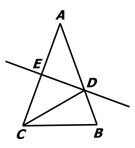
【题目】如图，△ABC≌△ADE，BC与DE交于点F．若∠BAE＝60°，∠DAC＝160°，则∠DFC的度数为____．
【答案】130°
【解析】
先根据全等三角形对应角相等求出∠BAC＝∠DAE，所以∠BAD＝∠CAE，然后求出∠BAD的度数，再根据∠B＝∠D，∠AGD＝∠FGB，可得∠DFB＝∠BAD，然后可求∠DFC的度数．
解：∵△ABC≌△ADE，
∴∠BAC＝∠DAE，∠B＝∠D，
又∵∠BAD＝∠DAE ∠BAE，∠CAE＝∠BAC ∠BAE，
∴∠BAD＝∠CAE，
∵∠DAC＝160°，∠BAE＝60°，
∴∠BAD＝
（∠DAC∠BAE）＝（160°60°）＝50°，
∵∠B＝∠D，∠AGD＝∠FGB，
∴∠DFB＝∠BAD＝50°，
∴∠DFC＝180°－50°＝130°，
故答案为：130°.
练习册系列答案
相关题目
【题目】某小组在学校组织的研究性学习活动中了解所居住的小区500户居民的人均收入情况，从中随机调查了40户居民家庭收入情况（收入取整数，单位：元），并绘制了如下的频数分布表和频数分布直方图，根据以上提供的信息，解答下列问题：
分组 | 频数 | 百分比 |
600≤x＜800 | 2 | 5% |
800≤x＜1000 | 6 | 15% |
1000≤x＜1200 | 45% | |
9 | 22.5% | |
1600≤x＜1800 | 2 | |
合计 | 40 | 100% |
（1）补全频数分布表．
（2）补全频数分布直方图．
（3）请你估计该居民小区家庭人均收入属于中等收入（1000≤x＜1600）的大约有多少户？
