Question

【题目】如图，在矩形ABCD中，AB=3，BC=6，对角线交于点O．将△BCD沿直线BD翻折，得到△BED．

（1）画出△BED，连接AE；

（2）求AE的长．

Answer 1

【答案】（1）、答案见解析；（2）、

【解析】

试题分析：（1）、首先根据题意得出图形；（2）、连接CE交BD于点F，根据折叠得出BD垂直平分CE，得出BD和OD的长度，根据cos∠EDB的值得出DF的长度，然后求出OF的长度，根据AE=2OF求出AE的长度.

试题解析：（1）、如图，补全图形．

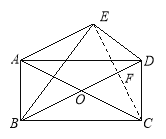
（2）、连接CE交BD于点F． ∵ 将△BCD沿直线BD翻折，得到△BED，∴ BD垂直平分CE．

∵ 矩形ABCD ，AB=3，BC=6， ∴ ，

∴ ∴ .

∵ ，∴ ． ∴

∴．∵BD垂直平分CE，O为AC中点，∴AE=2OF=．