题目内容
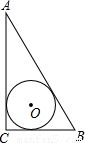
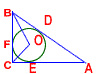
如图,⊙O内切于Rt△ABC,∠C=Rt∠,D、E、F是切点,若∠BOC=105°,AB=4cm,则∠OBC= ,∠BAC= ,BC= cm,AC= cm,内切圆半径r= cm.
【答案】分析:首先连接OF.根据角平分线的性质,可知∠BCO=∠OCA=45°,再多次利用直角三角形两直角边所对的角互余、角间的关系,求得∠OBC、∠BAC的度数.进而根据直角三角形中边角间的关系,求得BC、AC的长.利用直角三角形内切圆半径r=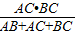 求得r的值.
求得r的值.
解答: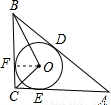 解:连接OF,
解:连接OF,
根据角平分线的性质,可知∠BCO=∠OCA=45°,
∴∠FOC=90°-∠BCO=90°-45°=45°,
∴∠BOF=∠BOC-∠FOC=105°-45°=60°,
在Rt△BFO中,∠FBO=90°-∠BOF=30°,
∴∠ABC=2∠FBO=60°,
∴∠A=90°-∠ABC=30°,
∵AB=4,
∴BC=AB•sin∠A=4× =2,
=2,
AC=AB•cos∠A=4×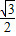 =
=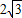 ,
,
内切圆半径r=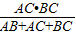 =
= =
=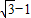 .
.
故答案为:30°,30°,2,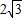 ,
,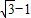 .
.
点评:本题考查三角形内切圆半径与内心.做好本题的关键是添加辅助线FO,建立起各角间的关系.
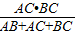 求得r的值.
求得r的值.解答:
 解:连接OF,
解:连接OF,根据角平分线的性质,可知∠BCO=∠OCA=45°,
∴∠FOC=90°-∠BCO=90°-45°=45°,
∴∠BOF=∠BOC-∠FOC=105°-45°=60°,
在Rt△BFO中,∠FBO=90°-∠BOF=30°,
∴∠ABC=2∠FBO=60°,
∴∠A=90°-∠ABC=30°,
∵AB=4,
∴BC=AB•sin∠A=4×
 =2,
=2,AC=AB•cos∠A=4×
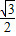 =
=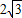 ,
,内切圆半径r=
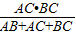 =
= =
=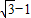 .
.故答案为:30°,30°,2,
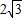 ,
,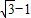 .
.点评:本题考查三角形内切圆半径与内心.做好本题的关键是添加辅助线FO,建立起各角间的关系.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
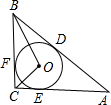 如图,⊙O内切于Rt△ABC,∠C=Rt∠,D、E、F是切点,若∠BOC=105°,AB=4cm,则∠OBC=
如图,⊙O内切于Rt△ABC,∠C=Rt∠,D、E、F是切点,若∠BOC=105°,AB=4cm,则∠OBC=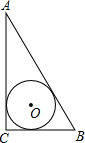 如图,⊙O内切于Rt△ABC,已知两直角边AC=4,BC=3,则⊙O的半径r=
如图,⊙O内切于Rt△ABC,已知两直角边AC=4,BC=3,则⊙O的半径r=