题目内容
四边形ABCD的对角线AC,BD相交于点C,下面四组条件
(1)AO=CO,BO=DO; (2)AO=CO=BO=DO;
(3)AO=CO,BO=DO,AC⊥BD; (4)AO=CO=BO=DO,AC⊥BD.
其中能判定ABCD是正方形的条件有
- A.(1)
- B.(2)
- C.(3)
- D.(4)
D
分析:根据正方形的性质与判定,(1)对角线相等的菱形是正方形,(2)对角线互相垂直的矩形是正方形,(3)对角线互相垂直平分且相等的四边形是正方形,(4)一组邻边相等,有三个角是直角的四边形是正方形,(5)一组邻边相等的矩形是正方形,(6)一组邻边相等且有一个角是直角的平行四边形是正方形,(7)四边均相等,对角线互相垂直平分且相等的四边形是正方形(8)有一个角为直角的菱形是正方形,(9)既是菱形又是矩形的四边形是正方形,逐个选项进行判断即可得出答案.
解答:(1)AO=CO,BO=DO;可判定四边形ABCD是平行四边形,不能判定它是正方形;
(2)AO=CO=BO=DO;可判定四边形ABCD是矩形,不能判定它是正方形;
(3)AO=CO,BO=DO,可判定四边形ABCD是平行四边形,再有AC⊥BD可判定它是菱形,不能判定它是正方形;
(4)AO=CO=BO=DO可判定四边形ABCD是矩形,再有AC⊥BD又可判定它是菱形,所以可以判定它是正方形.
故选:D.
点评:此题主要考查了正方形判定,掌握这些正方形的判定方法即可.
分析:根据正方形的性质与判定,(1)对角线相等的菱形是正方形,(2)对角线互相垂直的矩形是正方形,(3)对角线互相垂直平分且相等的四边形是正方形,(4)一组邻边相等,有三个角是直角的四边形是正方形,(5)一组邻边相等的矩形是正方形,(6)一组邻边相等且有一个角是直角的平行四边形是正方形,(7)四边均相等,对角线互相垂直平分且相等的四边形是正方形(8)有一个角为直角的菱形是正方形,(9)既是菱形又是矩形的四边形是正方形,逐个选项进行判断即可得出答案.
解答:(1)AO=CO,BO=DO;可判定四边形ABCD是平行四边形,不能判定它是正方形;
(2)AO=CO=BO=DO;可判定四边形ABCD是矩形,不能判定它是正方形;
(3)AO=CO,BO=DO,可判定四边形ABCD是平行四边形,再有AC⊥BD可判定它是菱形,不能判定它是正方形;
(4)AO=CO=BO=DO可判定四边形ABCD是矩形,再有AC⊥BD又可判定它是菱形,所以可以判定它是正方形.
故选:D.
点评:此题主要考查了正方形判定,掌握这些正方形的判定方法即可.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
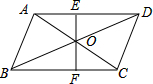 如图,EF过平行四边形ABCD的对角形的交点O,交AD于点E,交BC于点F,已知AB=5,BC=6,OE=2,那么四边形EFCD的周长是
如图,EF过平行四边形ABCD的对角形的交点O,交AD于点E,交BC于点F,已知AB=5,BC=6,OE=2,那么四边形EFCD的周长是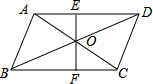 如图,EF过平行四边形ABCD的对角形的交点O,交AD于点E,交BC于点F,已知AB=5,BC=6,OE=2,那么四边形EFCD的周长是________.
如图,EF过平行四边形ABCD的对角形的交点O,交AD于点E,交BC于点F,已知AB=5,BC=6,OE=2,那么四边形EFCD的周长是________.