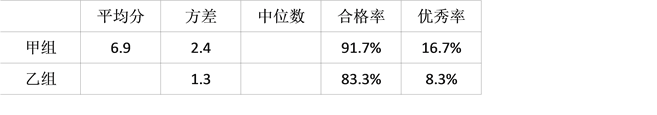题目内容
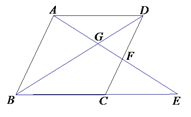
【题目】如图1,点![]() 是菱形
是菱形![]() 对角线的交点,已知菱形的边长为12,
对角线的交点,已知菱形的边长为12,![]() .
.
(1)求![]() 的长;
的长;
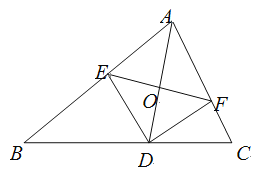
(2)如图2,点![]() 是菱形边上的动点,连结
是菱形边上的动点,连结![]() 并延长交对边于点
并延长交对边于点![]() ,将射线
,将射线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 交菱形于点
交菱形于点![]() ,延长
,延长![]() 交对边于点
交对边于点![]() .
.
①求证:四边形![]() 是平行四边形;
是平行四边形;
②若动点![]() 从点
从点![]() 出发,以每秒1个单位长度沿
出发,以每秒1个单位长度沿![]() 的方向在
的方向在![]() 和
和![]() 上运动,设点
上运动,设点![]() 运动的时间为
运动的时间为![]() ,当
,当![]() 为何值时,四边形
为何值时,四边形![]() 为矩形.
为矩形.
【答案】(1)![]() ;(2)①见解析;②
;(2)①见解析;②![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)解直角三角形求出BO即可解决问题;
(2)①想办法证明OE=OG,HO=FO即可解决问题;
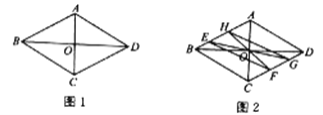
②分四种情形画出图形,(Ⅰ)如图1,当![]() 时,
时,![]() ,
,![]() 关于
关于![]() 对称,(Ⅱ)如图2,当
对称,(Ⅱ)如图2,当![]() ,
,![]() 关于
关于![]() 对称时,
对称时,![]() ,(Ⅲ)如图3,此时
,(Ⅲ)如图3,此时![]() 与图2中的
与图2中的![]() 的位置相同,(Ⅳ)如图4,当
的位置相同,(Ⅳ)如图4,当![]() ,
,![]() 关于
关于![]() 对称时,四边形EFGH是矩形.分别求解即可解决问题;
对称时,四边形EFGH是矩形.分别求解即可解决问题;
解:(1)∵四边形![]() 为菱形,
为菱形,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)①∵四边形ABCD是菱形,
∴AB∥CD,BO=OD,
∴∠EBO=∠GDO
∵∠BOE=∠DOG,
∴△EOB≌△GOD,
∴EO=GO,同理可得HO=FO,
∴四边形EFGH是平行四边形.
②由①得四边形![]() 为平行四边形,
为平行四边形,
∴当![]() 时,四边形
时,四边形![]() 为矩形.
为矩形.
(Ⅰ)如图1,当![]() 时,
时,![]() ,
,![]() 关于
关于![]() 对称.
对称.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
过点![]() 作
作![]() 于
于![]() 点,
点,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴ ,
,
∴![]() ,
,
∴![]() ;
;
(Ⅱ)如图2,当![]() ,
,![]() 关于
关于![]() 对称时,
对称时,![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() ;
;
(Ⅲ)如图3,此时![]() 与图2中的
与图2中的![]() 的位置相同,
的位置相同,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(Ⅳ)如图4,当![]() ,
,![]() 关于
关于![]() 对称时,
对称时,
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
综上所述,![]() 或
或![]() 或
或![]() 或
或![]() .
.
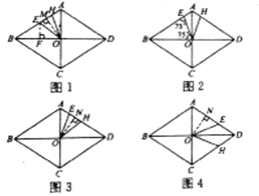

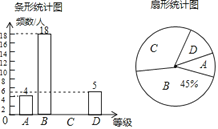
【题目】在学校组织的“迎新年,做守法好公民”的知识竞赛中,每班参加比赛的人数相同,成绩分为![]() 四个等级,其中相应等级的得分依次记为100分,90分,80分,70分.学校将某年级的1班和2班的成绩整理并绘制成如下的统计图:
四个等级,其中相应等级的得分依次记为100分,90分,80分,70分.学校将某年级的1班和2班的成绩整理并绘制成如下的统计图:
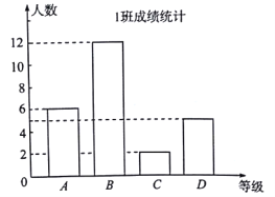

请你根据以上提供的信息解答下列问题:
(1)此次竞赛中,2班成绩在![]() 级以上(包括
级以上(包括![]() 级)的人数为____人;
级)的人数为____人;
(2)请你将表格补充完整:
班级 | 平均数(分) | 中位数(分) | 众数(分) |
1班 | 90 | ||
2班 | 87.6 | 100 |
(3)请从下列不同角度对这次竞赛成绩的结果进行分析;
①从平均数和中位数的角度来比较1班和2班的分成绩;
②从平均数和众数的角度来比较1班和2班的成绩;
③从![]() 级以上(包括
级以上(包括![]() 级)的人数的角度来比较1班和2班的成绩.
级)的人数的角度来比较1班和2班的成绩.