题目内容
(2008•毕节地区)已知△ABC的三条长分别为2cm,5cm,6cm,现将要利用长度为30cm和60cm的细木条各一根,做一个三角形木架与△ABC相似,要求以其中一根作为这个三角形木架的一边,将另一根截成两段(允许有余料,接头及损耗忽略不计)作为这个三角形木架的另外两边,那么这个三角形木架的三边长度分别为( )A.10cm,25cm,30cm
B.10cm,30cm,36cm或10cm,12cm,30cm
C.10cm,30cm,36cm
D.10cm,25cm,30cm或12cm,30cm,36cm
【答案】分析:所作的三角形与△ABC相似,则所作三角形的三边的比例关系也应该是2:5:6.设所作三角形的三边长分别为2a,5a,6a.题目要求以30cm和65cm其中一根为边,将另一根截成两段;因此长30cm的细木条必为其中一边,因此本题要分三种情况:①当2a=30cm时;②当5a=30cm时;③当6a=30cm时;然后再根据另外两边的和不能超过60cm为依据,将不合题意的解舍去.
解答:解:因为所作的三角形与△ABC相似,可设所作三角形的三边长为2a,5a,6a,
①当2a=30cm时,a=15cm,∴所作三角形的另外两边长为90cm和75cm,∵75>60,因此这种情况不成立;
②当5a=30cm时,a=6cm,∴所作三角形的另外两边长为12cm和36cm,12+36<60,因此这种情况成立;
③当6a=30cm时,a=5cm,∴所作三角形的另外两边长为10cm和25cm,10+25<60,因此这种情况成立.
综合三种情况可知:所作三角形的三边长为10cm,25cm,30cm或12cm,30cm,36cm.
故选D.
点评:本题从边的方面考查三角形,涉及分类讨论的思想方法.根据相似三角形的性质,正确求得所作三角形各边的长是解题的关键.
解答:解:因为所作的三角形与△ABC相似,可设所作三角形的三边长为2a,5a,6a,
①当2a=30cm时,a=15cm,∴所作三角形的另外两边长为90cm和75cm,∵75>60,因此这种情况不成立;
②当5a=30cm时,a=6cm,∴所作三角形的另外两边长为12cm和36cm,12+36<60,因此这种情况成立;
③当6a=30cm时,a=5cm,∴所作三角形的另外两边长为10cm和25cm,10+25<60,因此这种情况成立.
综合三种情况可知:所作三角形的三边长为10cm,25cm,30cm或12cm,30cm,36cm.
故选D.
点评:本题从边的方面考查三角形,涉及分类讨论的思想方法.根据相似三角形的性质,正确求得所作三角形各边的长是解题的关键.

练习册系列答案
相关题目
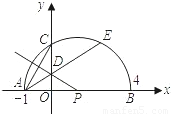
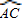 与
与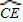 相等吗?请证明你的结论;
相等吗?请证明你的结论; AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.
AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.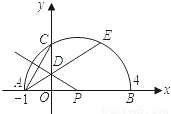
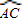 与
与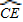 相等吗?请证明你的结论;
相等吗?请证明你的结论; AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.
AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.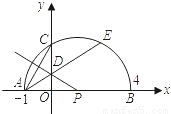
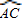 与
与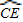 相等吗?请证明你的结论;
相等吗?请证明你的结论; AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.
AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.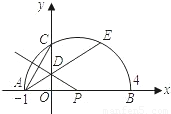
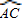 与
与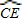 相等吗?请证明你的结论;
相等吗?请证明你的结论; AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.
AE,是否存在过点M的直线,使该直线与(1)中所得的抛物线的两个交点到y轴的距离相等?若存在,求出这条直线对应函数的解析式;若不存在.请说明理由.