题目内容
【题目】一个边长为4cm的等边三角形ABC与⊙O等高,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长为 cm.
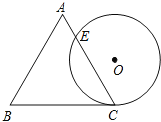
【答案】3
【解析】
试题分析:连接OC,并过点O作OF⊥CE于F,根据等边三角形的性质,等边三角形的高等于底边的![]() 倍.已知边长为4cm的等边三角形ABC与⊙O等高,说明⊙O的半径为
倍.已知边长为4cm的等边三角形ABC与⊙O等高,说明⊙O的半径为![]() ,即OC=
,即OC=![]() ,又∠ACB=60°,故有∠OCF=30°,在Rt△OFC中,可得出FC的长,利用垂径定理即可得出CE的长.
,又∠ACB=60°,故有∠OCF=30°,在Rt△OFC中,可得出FC的长,利用垂径定理即可得出CE的长.
解:连接OC,并过点O作OF⊥CE于F,
且△ABC为等边三角形,边长为4,
故高为2![]() ,即OC=
,即OC=![]() ,
,
又∠ACB=60°,故有∠OCF=30°,
在Rt△OFC中,可得FC=OCcos30°=![]() ,
,
OF过圆心,且OF⊥CE,根据垂径定理易知CE=2FC=3.
故答案为:3.


练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目

